题目内容
已知函数f(x)=ax2-c,-4≤f(1)≤-1,-1≤f(2)≤5.求f(3)的取值范围.
思路分析:利用f(1)与f(2)设法表示出a,c,然后再代入f(3)的表达式中,从而用f(1)与f(2)来表示f(3),最后运用已知条件确定f(3)的取值范围.也可用线性规划求解.
解:∵f(x)=ax2-c,?
∴![]() 即
即![]()
解得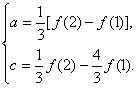
∴f(3)=9a-c=![]() f(2)-
f(2)-![]() f(1).?
f(1).?
又∵-4≤f(1)≤-1,-1≤f(2)≤5,?
∴![]() ≤-
≤-![]() f(1)≤
f(1)≤![]() , ①
, ①
-![]() ≤
≤![]() f(2)≤
f(2)≤![]() . ②
. ②
把①②式的两边分别相加得?
-1≤![]() f(2)-
f(2)- ![]() f(1)≤20,?
f(1)≤20,?
即-1≤f(3)≤20.
温馨提示
在利用不等式基本性质求范围时,一定要强调不等式性质中条件的作用,不等式的两边同乘以(或除以)一个含有字母的式子,一定要知道它的值是正还是负,并且不能为零,才能得到正确的结论.同向不等式只能相加,不能相减.

练习册系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |