题目内容
过抛物线y2=2x的对称轴上的定点M(m,0),(m>0),作直线AB交抛物线于A,B两点.(1)试证明A,B两点的纵坐标之积为定值;
(2)若△OAB的面积的最小值为4,求m的值.
【答案】分析:(1)设lAB:x=ty+m代入y2=2x得y2-2ty-2m=0,设A(x1,y1),B(x2,y2)从而可得,y1y2=-2m
(2)由于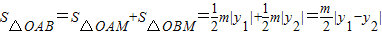 ll=
ll=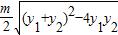 ,结合方程的根与系数的关系及二次函数的性质可求m
,结合方程的根与系数的关系及二次函数的性质可求m
解答:解:(1)设lAB:x=ty+m代入y2=2x得y2-2ty-2m=0,设A(x1,y1),B(x2,y2)
△=4t2+8m>0,y1+y2=2t,y1y2=-2m
∵m为常数∴y1•y2=-2m为定值
(2)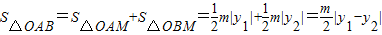 =
=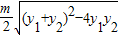 =
=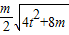
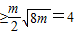
∴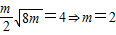
点评:本题主要考查了直线与曲线位置关系的应用,常联立方程组转化为方程的根与系数的关系,而弦长公式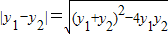 的应用是解决本题的关键
的应用是解决本题的关键
(2)由于
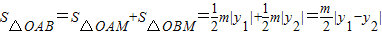 ll=
ll=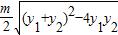 ,结合方程的根与系数的关系及二次函数的性质可求m
,结合方程的根与系数的关系及二次函数的性质可求m解答:解:(1)设lAB:x=ty+m代入y2=2x得y2-2ty-2m=0,设A(x1,y1),B(x2,y2)
△=4t2+8m>0,y1+y2=2t,y1y2=-2m
∵m为常数∴y1•y2=-2m为定值
(2)
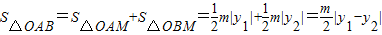 =
=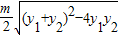 =
=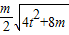
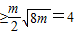
∴
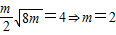
点评:本题主要考查了直线与曲线位置关系的应用,常联立方程组转化为方程的根与系数的关系,而弦长公式
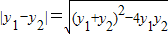 的应用是解决本题的关键
的应用是解决本题的关键 
练习册系列答案
相关题目
过抛物线y2=2x的焦点F作直线l交抛物线于A、B两点,若
-
=1,则直线l的倾斜角θ(0<θ≤
)等于( )
| 1 |
| |AF| |
| 1 |
| |BF| |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
过抛物线y2=2x的焦点作一条直线与抛物线交于两点,它们的横坐标之和等于2,则这样的直线( )
| A、有且只有一条 | B、有且只有两条 | C、有且只有三条 | D、有且只有四条 |