题目内容
(本小题共14分)函数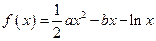 ,
,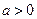 ,
,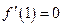 .
.
(1)①试用含有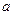 的式子表示
的式子表示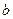 ;②求
;②求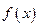 的单调区间;
的单调区间;
(2)对于函数图像上的不同两点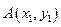 ,
,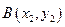 ,如果在函数图像上存在点
,如果在函数图像上存在点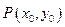 (其中
(其中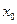 在
在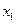 与
与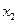 之间),使得点
之间),使得点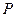 处的切线
处的切线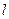 ∥
∥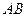 ,则称
,则称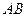 存在“伴随切线”,当
存在“伴随切线”,当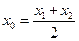 时,又称
时,又称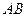 存在“中值伴随切线”。试问:在函数
存在“中值伴随切线”。试问:在函数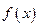 的图像上是否存在两点
的图像上是否存在两点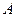 、
、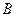 ,使得
,使得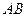 存在“中值伴随切线”?若存在,求出
存在“中值伴随切线”?若存在,求出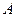 、
、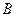 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
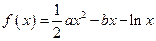 ,
,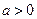 ,
,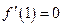 .
.(1)①试用含有
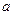 的式子表示
的式子表示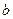 ;②求
;②求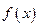 的单调区间;
的单调区间;(2)对于函数图像上的不同两点
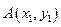 ,
,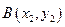 ,如果在函数图像上存在点
,如果在函数图像上存在点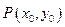 (其中
(其中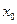 在
在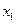 与
与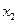 之间),使得点
之间),使得点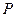 处的切线
处的切线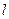 ∥
∥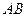 ,则称
,则称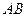 存在“伴随切线”,当
存在“伴随切线”,当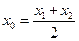 时,又称
时,又称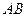 存在“中值伴随切线”。试问:在函数
存在“中值伴随切线”。试问:在函数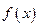 的图像上是否存在两点
的图像上是否存在两点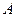 、
、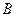 ,使得
,使得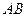 存在“中值伴随切线”?若存在,求出
存在“中值伴随切线”?若存在,求出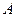 、
、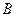 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。(1)
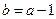 ,
,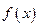 增区间为
增区间为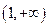 ,减区间为
,减区间为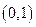
(2)不存在
解:(1)①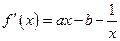 ∵
∵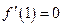 ∴
∴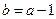 . (2分)
. (2分)
②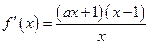 ∵
∵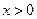 ,
,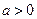 ∴当
∴当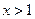 时
时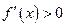 ,
,
当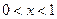 时,
时,
∴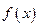 增区间为
增区间为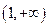 ,减区间为
,减区间为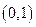
(2)不存在 (7分) (反证法)
若存在两点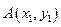 ,
,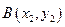 ,不妨设
,不妨设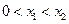 ,则
,则
曲线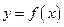 在
在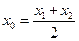 的切线斜率
的切线斜率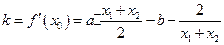
又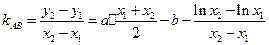
∴由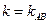 得
得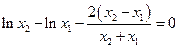 ①
①
法一:令
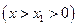
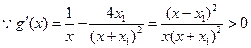
∴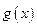 在
在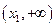 上为增函数
上为增函数
又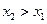 ∴
∴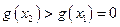 与①矛盾
与①矛盾
∴不存在 (16分)
法二:令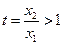 ,则①化为
,则①化为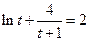 ②
②
令
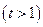 ∵
∵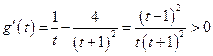
∴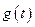 在
在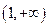 为增函数
为增函数
又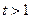 ∴
∴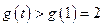 此与②矛盾,∴不存在
此与②矛盾,∴不存在
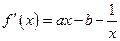 ∵
∵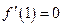 ∴
∴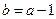 . (2分)
. (2分)②
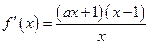 ∵
∵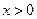 ,
,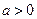 ∴当
∴当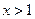 时
时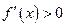 ,
,当
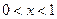 时,
时,
∴
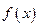 增区间为
增区间为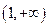 ,减区间为
,减区间为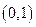
(2)不存在 (7分) (反证法)
若存在两点
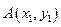 ,
,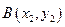 ,不妨设
,不妨设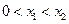 ,则
,则曲线
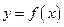 在
在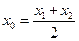 的切线斜率
的切线斜率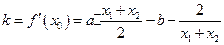
又
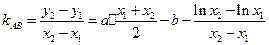
∴由
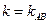 得
得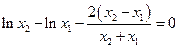 ①
① 法一:令

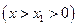
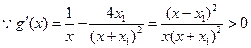
∴
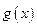 在
在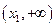 上为增函数
上为增函数 又
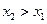 ∴
∴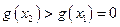 与①矛盾
与①矛盾∴不存在 (16分)
法二:令
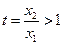 ,则①化为
,则①化为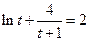 ②
②令

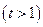 ∵
∵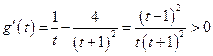
∴
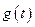 在
在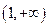 为增函数
为增函数 又
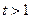 ∴
∴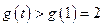 此与②矛盾,∴不存在
此与②矛盾,∴不存在
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目

 ,
, ,
, ,则
,则 ( )
( )
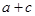


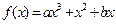 (其中常数a,b∈R),
(其中常数a,b∈R),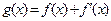 是奇函数.
是奇函数.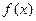 的表达式;(2)讨论
的表达式;(2)讨论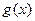 的单调性,并求
的单调性,并求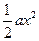 +
+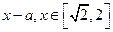 其中a为实数
其中a为实数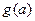
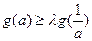 恒成立,求实数
恒成立,求实数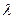 的取值范围。
的取值范围。 ),(m,y
),(m,y ),(m+1,y
),(m+1,y )都在二次函数y=x
)都在二次函数y=x -2x的图像上,
-2x的图像上,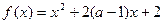 在区间
在区间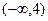 上是减函数,则实数
上是减函数,则实数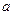 的取值范围是____________.
的取值范围是____________.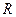 上的函数
上的函数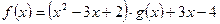 ,其中,函数
,其中,函数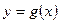 的图像是一条连续曲线,则方程
的图像是一条连续曲线,则方程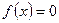 在下面哪个范围内必有实数根( )
在下面哪个范围内必有实数根( )

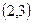
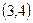
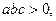 二次函数
二次函数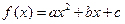 的图象可能是 ( )
的图象可能是 ( )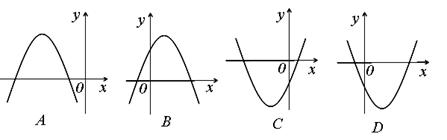
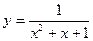 的最大值是 ( )
的最大值是 ( )


