题目内容
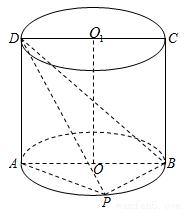
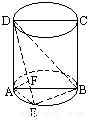
如图,ABCD是圆柱的轴截面,点E在底面的圆周上,AF⊥DE,F是垂足.(1)求证:AF⊥DB;
(2)如果AB=a,圆柱与三棱锥D-ABE的体积比等于3π,求点E到截面ABCD的距离.
【答案】分析:(1)要证AF⊥DB,只需证明AF垂直DB所在的平面DEB,即证明AF垂直平面DEB内的两条相交直线EB、DE即可.
(2)如果AB=a,设点E到平面ABCD的距离为d,记AD=h,求出圆柱体积求出三棱锥D-ABE的体积,它们的比等于3π,然后求点E到截面ABCD的距离.
解答: (1)证明:根据圆柱性质,DA⊥平面ABE,
(1)证明:根据圆柱性质,DA⊥平面ABE,
∵EB?平面ABE,
∴DA⊥EB,
∵AB是圆柱底面的直径,点E在圆周上,
∴AE⊥EB,又AE∩AD=A,故得EB⊥平面DAE,
∵AF?平面DAE,
∴EB⊥AF,
又AF⊥DE,且EB∩DE=E,故得AF⊥平面DEB,
∵DB?平面DEB,
∴AF⊥DB.
(2)解:设点E到平面ABCD的距离为d,记AD=h,因圆柱轴截面ABCD是矩形,所以AD⊥AB.
S△ABD= AB•AD=
AB•AD=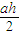
∴VD-ABE=VE-ABD=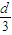 S△ABD=
S△ABD= dah
dah
又V圆柱= a2h
a2h
由题设知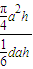 =3π,即d=
=3π,即d= .
.
点评:本题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力,计算能力,是中档题.
(2)如果AB=a,设点E到平面ABCD的距离为d,记AD=h,求出圆柱体积求出三棱锥D-ABE的体积,它们的比等于3π,然后求点E到截面ABCD的距离.
解答:
 (1)证明:根据圆柱性质,DA⊥平面ABE,
(1)证明:根据圆柱性质,DA⊥平面ABE,∵EB?平面ABE,
∴DA⊥EB,
∵AB是圆柱底面的直径,点E在圆周上,
∴AE⊥EB,又AE∩AD=A,故得EB⊥平面DAE,
∵AF?平面DAE,
∴EB⊥AF,
又AF⊥DE,且EB∩DE=E,故得AF⊥平面DEB,
∵DB?平面DEB,
∴AF⊥DB.
(2)解:设点E到平面ABCD的距离为d,记AD=h,因圆柱轴截面ABCD是矩形,所以AD⊥AB.
S△ABD=
 AB•AD=
AB•AD=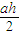
∴VD-ABE=VE-ABD=
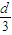 S△ABD=
S△ABD= dah
dah又V圆柱=
 a2h
a2h由题设知
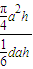 =3π,即d=
=3π,即d= .
.点评:本题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力,计算能力,是中档题.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
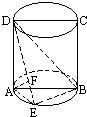 如图,ABCD是圆柱的轴截面,点E在底面的圆周上,AF⊥DE,F是垂足.
如图,ABCD是圆柱的轴截面,点E在底面的圆周上,AF⊥DE,F是垂足.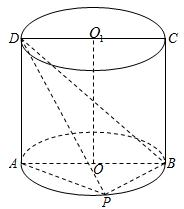 如图,ABCD是底面半径为1的圆柱OO1的轴截面,P是下底面圆周上一点(异于A、B)
如图,ABCD是底面半径为1的圆柱OO1的轴截面,P是下底面圆周上一点(异于A、B)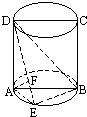 如图,ABCD是圆柱的轴截面,点E在底面的圆周上,AF⊥DE,F是垂足.
如图,ABCD是圆柱的轴截面,点E在底面的圆周上,AF⊥DE,F是垂足.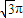 ,求二面角B-AD-P的大小.
,求二面角B-AD-P的大小.