题目内容
给出四个函数,分别满足①f(x+y)=f(x)+f(y),②g(x+y)=g(x)·g(y),③h(x·y)=h(x)+h(y),④m(x·y)=m(x)·m(y).又给出四个函数的图像,那么正确的匹配方案可以是 ( )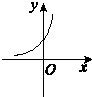
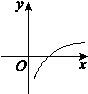
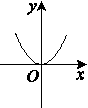
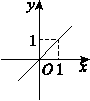
甲 乙 丙 丁
| A.①甲,②乙,③丙,④丁 | B.①乙,②丙,③甲,④丁 |
| C.①丙,②甲,③乙,④丁 | D.①丁,②甲,③乙,④丙 |
D
解析试题分析::①f(x)=x,这个函数可使 f(x+y)=x+y=f(x)+f(y)成立,
∵f(x+y)=x+y,x+y=f(x)+f(y),∴f(x+y)=f(x)+f(y),自变量的和等于因变量的和.
正比例函数y=kx就有这个特点.故①-丁;②寻找一类函数g(x),使得g(x+y)=g(x)g(y),即自变量相加等于因变量乘积.指数函数y=ax(a>0,a≠1)具有这种性质:g(x)=ax,g(y)=ay,g(x+y)=ax+y=ax•ay=g(x)•g(y).故②-甲;③自变量的乘积等于因变量的和:与②相反,可知对数函数具有这种性质:
令:h(x)=logax,则h(xy)=loga(xy)=logax+logbx.故③-乙.④t(x)=x2,这个函数可使t(xy)=t(x)t(y)成立.∵t(x)=x2,∴t(xy)=(xy)2=x2y2=t(x)t(y),故④-丙.故选D.
考点:1.对数函数、指数函数的图像与性质;2.一次函数的性质与图象.

练习册系列答案
相关题目
三个数 ,
, 之间的大小关系是
之间的大小关系是
A. | B. | C. | D. |
已知幂函数y=f(x)的图象过点( ),则log2f(2)的值为( )
),则log2f(2)的值为( )
A. | B.- | C.2 | D.-2 |
函数 的零点所在区间为( )
的零点所在区间为( )
| A.(3,+∞) | B.(2,3) | C.(1,2) | D.(0,1) |
已知函数 ,则
,则 ( )
( )
| A.0 | B.1 | C.-2 | D.-1 |
设 ,则函数
,则函数 的值域是( ).
的值域是( ).
A. | B. | C. | D. |
函数 的零点所在的区间为( )
的零点所在的区间为( )
| A.(1,2) | B.(2,3) | C.(3,4) | D.(4,5) |
 的定义域为
的定义域为 ,若存在非零实数
,若存在非零实数 ,使得对于任意
,使得对于任意 有
有 且
且 ,则称
,则称 上的
上的 的函数
的函数 ,且
,且 度低调函数,那么实数
度低调函数,那么实数 的取值范围是( )
的取值范围是( )

 且
且 ,函数
,函数 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )