Question

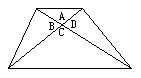
梯形的两条对角线把梯形分成四部分，用五种不同颜色给这四部分涂色，每一部分涂一种颜色，任何相邻(具有公共边)的两部分涂不同颜色，问有多少种不同的涂色方法？

Answer 1

答案：
解析：

解 符合要求的涂色至少要两种颜色．所以可以分成三类方法涂色： 　　(1)用四种颜色涂色，有＝120种方法； 　　(2)用三种颜色涂色，选三种颜色的方法有种；区域A，C或B，D有一组涂同色，另一组涂2色有种，根据乘法原理，得120种； 　　(3)用两种颜色涂色，选两种颜色有种，A，C与B，D各涂一色有＝20种方法． 　　根据加法原理，共有涂色方法120＋120＋20＝260种．