题目内容
“a=1”是“函数 在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
在其定义域上为奇函数”的________条件.(填“充分不必要”“必要不充分”“充要”或“既不充分也不必要”)
充分不必要
分析:当a=1时,函数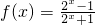 ,其定义域为R,f(-x)=
,其定义域为R,f(-x)= =
= =
= =-f(x),可得f(x)为奇函数;但反之不成立,因为当a=-1时也能使函数为奇函数.
=-f(x),可得f(x)为奇函数;但反之不成立,因为当a=-1时也能使函数为奇函数.
解答:当a=1时,函数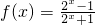 ,其定义域为R,
,其定义域为R,
f(-x)= =
= =
= =-f(x),可得f(x)为奇函数;
=-f(x),可得f(x)为奇函数;
“函数 在其定义域上为奇函数”不能推出“a=1”,
在其定义域上为奇函数”不能推出“a=1”,
因为当a=-1时, ,其定义域为{x|x≠0},
,其定义域为{x|x≠0},
f(-x)= =
= =
= =-f(x),也可得f(x)为奇函数.
=-f(x),也可得f(x)为奇函数.
故“a=1”是“函数 在其定义域上为奇函数”的充分不必要条件.
在其定义域上为奇函数”的充分不必要条件.
故答案为:充分不必要.
点评:本题为充要条件的判断,熟练掌握证明函数的奇偶性的方法是解决问题的关键,属基础题.
分析:当a=1时,函数
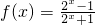 ,其定义域为R,f(-x)=
,其定义域为R,f(-x)= =
= =
= =-f(x),可得f(x)为奇函数;但反之不成立,因为当a=-1时也能使函数为奇函数.
=-f(x),可得f(x)为奇函数;但反之不成立,因为当a=-1时也能使函数为奇函数.解答:当a=1时,函数
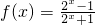 ,其定义域为R,
,其定义域为R,f(-x)=
 =
= =
= =-f(x),可得f(x)为奇函数;
=-f(x),可得f(x)为奇函数;“函数
 在其定义域上为奇函数”不能推出“a=1”,
在其定义域上为奇函数”不能推出“a=1”,因为当a=-1时,
 ,其定义域为{x|x≠0},
,其定义域为{x|x≠0},f(-x)=
 =
= =
= =-f(x),也可得f(x)为奇函数.
=-f(x),也可得f(x)为奇函数.故“a=1”是“函数
 在其定义域上为奇函数”的充分不必要条件.
在其定义域上为奇函数”的充分不必要条件.故答案为:充分不必要.
点评:本题为充要条件的判断,熟练掌握证明函数的奇偶性的方法是解决问题的关键,属基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
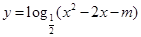 的值域为R;
的值域为R;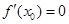 ,则函数y=f(x)在x=x0处取得极值;
,则函数y=f(x)在x=x0处取得极值; 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。 在定义域上是奇函数的充分不必要条件.
在定义域上是奇函数的充分不必要条件.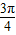 个单位可得到y=sin2x的图象.
个单位可得到y=sin2x的图象.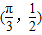 是函数
是函数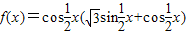 图象的一个对称中心.
图象的一个对称中心.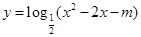 的值域为R;
的值域为R;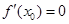 ,则函数y=f(x)在x=x0处取得极值;
,则函数y=f(x)在x=x0处取得极值; 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。 ,则函数y=f(x)在x=x0处取得极值;
,则函数y=f(x)在x=x0处取得极值; 的值域为R;
的值域为R; 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。 在
在 单调递增”的
单调递增”的