题目内容
“n=10”是“(
+
)n”的展开式中有常数项的（ ）
| x |
| 1 | |||
|
分析：利用二项展开式的通项公式求出第r+1项，令x的指数为0求出常数项列出方程求出n，r的关系，进而根据必要条件、充分条件与充要条件的判断可得答案．
解答：解：Tr+1=Cnr（
）n-r（
）r=Cnrx
令
=0，
∴3n=5r．
∴n必为5的倍数，
∴“n=10”是“(
+
)n”的展开式中有常数项；反之不成立．
故“n=10”是“(
+
)n”的展开式中有常数项的充分不必要条件．
故选A．
| x |
| 1 | |||
|
| 3n-5r |
| 6 |
令
| 3n-5r |
| 6 |
∴3n=5r．
∴n必为5的倍数，
∴“n=10”是“(
| x |
| 1 | |||
|
故“n=10”是“(
| x |
| 1 | |||
|
故选A．
点评：本题考查必要条件、充分条件与充要条件的判断，考查二项展开式的通项公式是解决二项展开式的特点项问题的工具．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
某校高一年级共有学生320人．为调查高一年级学生每天晚自习自主支配学习时间（指除了完成教师布置的作业后学生根据自己的需要进行学习的时间）情况，学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查．根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据（单位：分钟），按照以下区间分为七组：①[0，10），②[10，20），③[20，30），④[30，40），⑤[40，50），⑥[50，60），⑦[60，70），得到频率分布直方图如图．已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人．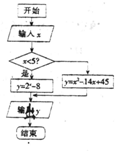
从{1，2，3，…n}（n∈N*）中随机取出一个数x，按程序框图所给算法输出y．