题目内容
已知双曲线关于两坐标轴对称,且与圆x2+y2=10相交于点P(3,-1),若此圆过点P的切线与双曲线的渐近线平行,求此双曲线的方程.解法一:切点为P(3,-1)的圆的切线方程为3x-y=10,
∵双曲线的一条渐近线与此切线平行,且双曲线关于两坐标轴对称,
∴两条渐近线方程为3x±y=0.
设所求的双曲线方程为9x2-y2=λ(λ≠0).
∵点P(3,-1)在所求的双曲线上,∴λ=80.
∴所求双曲线的方程为
解法二:
切点为P(3,-1)的圆的切线方程为3x-y=10,
∵双曲线的一条渐近线与此切线平行,且双曲线关于两坐标轴对称,
∴双曲线的渐近线方程为3x±y=0.
当双曲线的焦点在x轴上时,设双曲线方程为![]() (a>0,b>0),则其渐近线方程为y=±
(a>0,b>0),则其渐近线方程为y=±![]() x,即
x,即![]() =3,则双曲线方程可化为
=3,则双曲线方程可化为![]() .
.
∵双曲线过点P(3,-1),
∴![]()
∴所求双曲线的方程为
当焦点在y轴上时,设双曲线方程为![]() (a>0,b>0),则其渐近线方程为y=±
(a>0,b>0),则其渐近线方程为y=±![]() x,即
x,即![]() =3,则双曲线方程可化为
=3,则双曲线方程可化为![]()
∵双曲线过点P(3,-1),∴![]()
得-![]() ,此时方程无解.
,此时方程无解.
∴所求的双曲线方程为

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,且与椭圆
,且与椭圆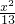 +
+ =1有共同的焦点,求该双曲线的方程.
=1有共同的焦点,求该双曲线的方程.