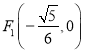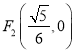题目内容
【题目】设函数![]() (
(![]() ,且
,且![]() ),
),![]() ,(其中
,(其中![]() 为
为![]() 的导函数).
的导函数).
(1)当![]() 时,求
时,求![]() 的极大值点;
的极大值点;
(2)讨论![]() 的零点个数.
的零点个数.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)令![]() 求出
求出![]() 的极值点,判断
的极值点,判断![]() 的符号变化即可得出答案;
的符号变化即可得出答案;
(2)对a和x进行讨论,利用零点的存在性定理,结合函数的图象判断零点的个数.
试题解析:
(1)![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,故
,故![]() 的极大值点为
的极大值点为![]() ;
;
(2)(i)先考虑![]() 时,
时, ![]() 的零点个数,当
的零点个数,当![]() 时,
时, ![]() 为单减函数,
为单减函数,
![]() ;
; ![]() ,由零点存在性定理知
,由零点存在性定理知![]() 有一个零点;
有一个零点;
当![]() 时,由
时,由![]() 得
得
![]() ,令
,令![]() ,则
,则![]() .
.
由![]() 得,
得, ![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
故![]() ,
, ![]() ,且
,且![]() 总成立,故
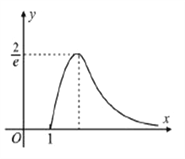
总成立,故![]() 的图像如下图,
的图像如下图,
由数形结合知,
②若![]() 即
即![]() 时,当
时,当![]() 时,
时, ![]() 无零点,故
无零点,故![]() 时,
时, ![]() 有一个零点;
有一个零点;
②若![]() 即
即![]() 时,当
时,当![]() 时,
时, ![]() 有一个零点,故
有一个零点,故![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
③若![]() 即
即![]() ,当
,当![]() 时,
时, ![]() 有
有![]() 个零点,故
个零点,故![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.
(ii)再考虑![]() 的情形,若
的情形,若![]() ,则
,则![]() ,同上可知,
,同上可知,
当![]() 即
即![]() 时,
时, ![]() 有一个零点;
有一个零点;
当![]() 即
即![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
当![]() 即
即![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.
综合上述,
①当![]() 或
或![]() 时,
时, ![]() 有一个零点;
有一个零点;
②当![]() 或
或![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
③当![]() 或
或![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.

练习册系列答案
相关题目