题目内容
已知P(a,b)是圆x2+y2=r2外一定点,PA、PB是过P点的该圆的两条切线,A、B为切点.求证:直线AB的方程为ax+by=r2.
证法一:设点A、B的坐标分别为(x1,y1)、(x2,y2),则过A、B两点的切线方程分别为
∵P点在两条切线上,故(a,b)满足方程(1)(2),即
由(3)(4)(x1,y1)、B(x2,y2)是直线ax+by=r2上的点,由已知,得A、B是两个不重合的点,两点确定一条直线,故ax+by=r2就是直线AB的方程.
证法二:如图所示,A、O、B、P四点共面,且以OP为直径的圆的方程为(x-![]() a)2+(y-
a)2+(y-![]() b)2=
b)2=
![]() (a2+b2),
(a2+b2),

即x2+y2-ax-by=0. (5)
又圆的方程为x2+y2=r2, (6)
由(6)-(5),得ax+by=r2即为过切点A、B的直线方程.

练习册系列答案
相关题目
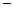
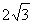
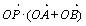
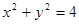 上满足条件
上满足条件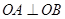 的两个点,其中O是坐标原点,
的两个点,其中O是坐标原点, 分别过A、B作
分别过A、B作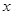 轴的垂线段,交椭圆
轴的垂线段,交椭圆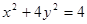 于
于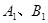 点,动点P满足
点,动点P满足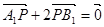 .(1)求动点P的轨迹方程;(2)设S1和S2
.(1)求动点P的轨迹方程;(2)设S1和S2 分别表示
分别表示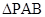 和
和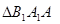 的面积,当点P在x轴的上方,点A在x轴的下方时,求
的面积,当点P在x轴的上方,点A在x轴的下方时,求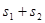 的最大值。
的最大值。 的圆上两点,且
的圆上两点,且 ,则
,则 等于( )
等于( )


 的圆上两点,且
的圆上两点,且 ,则
,则 等于( )
等于( )

