题目内容
已知函数![]() 是R上的奇函数,当
是R上的奇函数,当![]() 时,
时,![]() 取得极值-2(1)求函数
取得极值-2(1)求函数![]() 的解析式;(2)当
的解析式;(2)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
解析:
(I)由![]() 是R上的奇函数,有
是R上的奇函数,有![]() ,所以
,所以![]() 因此
因此![]()
对函数![]() 求导得
求导得![]() 由题意得
由题意得![]()
所以![]() 解得
解得![]()
![]() 因此
因此![]() (6分)
(6分)
(Ⅱ)![]() 令
令![]() ,得
,得![]() 或
或![]()
当![]() 变化时,
变化时,![]() 、
、![]() 的变化如下表:
的变化如下表:
|
|
|
|
|
| 1 | (1,3) | 3 |
|
|
| 0 |
| 0 |
| ||
|
|
| 增 |
| 减 |
| 增 | 18 |
从上表可知,![]() 在区间
在区间![]() 上的最大值是18。
上的最大值是18。
原命题等价于![]() 大于
大于![]() 在
在![]() 上的最大值,所以
上的最大值,所以![]() 。故
。故![]() 的取值范围是
的取值范围是![]() (12分)
(12分)

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 ,满足
,满足 ,且在区间[0,2]上是增函
,且在区间[0,2]上是增函 B.
B.

 D.
D.

 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上 ,则
,则 ;[来源:Z§xx§k.Com]
;[来源:Z§xx§k.Com] 且
且 ;
; 在[-8,8]内恰有四个不同的根
在[-8,8]内恰有四个不同的根 ,则
,则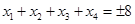 ;
; ,满足
,满足 ,且在区间[0,1]上是增函
,且在区间[0,1]上是增函 在区间
在区间 上有四个不同的根
上有四个不同的根 ,则
,则 ( )
( ) (B)
(B) (C)
(C)  (D)
(D)