题目内容
已知函数f(x)=loga(Ⅰ)判定f(x)的单调性,并证明;
(Ⅱ)设g(x)=1+loga(x-1),若方程f(x)=g(x)有实根,求a的取值范围;
(Ⅲ)求函数h(x)=f(x)lna+ln(x+3)-![]() 在[4,6]上的最大值和最小值.
在[4,6]上的最大值和最小值.
解:(Ⅰ)由![]() >0,得x<-3或x>3,
>0,得x<-3或x>3,
任取x1<x2<-3.
则f(x1)-f(x2)=loga![]() -loga
-loga![]() =loga
=loga![]() .
.
∵(x1-3)(x2+3)-(x1+3)(x2-3)=10(x1-x2)<0,
又(x1-3)(x2+3)>0且(x1+3)(x2-3)>0,
0<![]() <1,
<1,
∴当a>1时,f(x1)-f(x2)<0,
∴f(x)单调递增,
当0<a<1时,f(x1)-f(x2)>0,
∴f(x)单调递减.
(Ⅱ)若f(x)=g(x)有实根,即:loga ![]() =1+loga(x-1).
=1+loga(x-1).
∴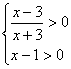
![]() x>3.
x>3.
∴即方程:![]() =a(x-1)有大于3的实根.
=a(x-1)有大于3的实根.
a=![]() (∵x>3)
(∵x>3)
=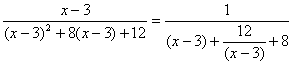 ≤
≤![]() .
.
“=”当且仅当x-3=![]() 即当x=3+2
即当x=3+2![]() 时成立,∴a∈(0,
时成立,∴a∈(0,![]() ).
).
(Ⅲ)h(x)=f(x)lna+ln(x+3)-![]() =ln(x-3)-
=ln(x-3)-![]() .
.
h′(x)=![]() ,由
,由![]() =0有x2-3x-4=0,解得x1=4;x2=-1(舍去).
=0有x2-3x-4=0,解得x1=4;x2=-1(舍去).
当x∈[4,6]时,h′(x)<0,h(x)单调递减;
所以函数h(x)在[4,6]上的最小值为h(6)=ln3-4,最大值为h(4)=-2.

练习册系列答案
相关题目