题目内容
已知函数 .
.(1)若函数f(x)在[1,+∞)上单调递增,求实数a的取值范围.
(2)记函数g(x)=x2[f′(x)+2x-2],若g(x)的最小值是-6,求函数f(x)的解析式.
【答案】分析:(1)由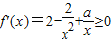 ,知
,知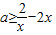 在[1,+∞)上恒成立,构造函数
在[1,+∞)上恒成立,构造函数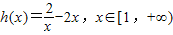 ,利用导数性质,能求出实数a的取值范围.
,利用导数性质,能求出实数a的取值范围.
(2)由g(x)=2x3+ax-2,x>0,知g′(x)=6x2+a,由a≥0时,g′(x)≥0恒成立知a<0,由此能求出函数f(x)的解析式.
解答:(本小题满分14分)
解:(1)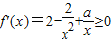 ,
,
∴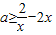 在[1,+∞)上恒成立…(2分)
在[1,+∞)上恒成立…(2分)
令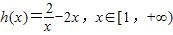
∵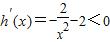 恒成立,
恒成立,
∴h(x)在[1,+∞)单调递减…(4分)
h(x)max=h(1)=0…(6分)
∴a≥0,
故实数a的取值范围为[0,+∞).…(7分)
(2)g(x)=2x3+ax-2,x>0
∵g′(x)=6x2+a…(9分)
当a≥0时,g′(x)≥0恒成立,
∴g(x)在(0,+∞)单调递增,无最小值,不合题意,
∴a<0.…(11分)
令g′(x)=0,则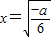 (舍负)
(舍负)
∵0<x<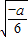 时,g′(x)<0;x>
时,g′(x)<0;x>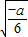 时,g′(x)>0,
时,g′(x)>0,
∴g(x)在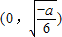 上单调递减,在
上单调递减,在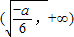 上单调递增,
上单调递增,
则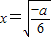 是函数的极小值点.
是函数的极小值点.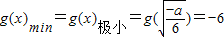 .…(13分)
.…(13分)
解得a=-6,
故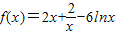 .…(14分)
.…(14分)
点评:本题考查函数是增函数时实数的取值范围的求法,考查函数的解析式的求法,解题时要认真审题,仔细解答,注意导数性质的合理运用.
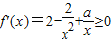 ,知
,知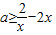 在[1,+∞)上恒成立,构造函数
在[1,+∞)上恒成立,构造函数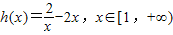 ,利用导数性质,能求出实数a的取值范围.
,利用导数性质,能求出实数a的取值范围.(2)由g(x)=2x3+ax-2,x>0,知g′(x)=6x2+a,由a≥0时,g′(x)≥0恒成立知a<0,由此能求出函数f(x)的解析式.
解答:(本小题满分14分)
解:(1)
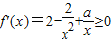 ,
,∴
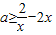 在[1,+∞)上恒成立…(2分)
在[1,+∞)上恒成立…(2分)令
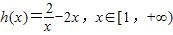
∵
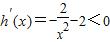 恒成立,
恒成立,∴h(x)在[1,+∞)单调递减…(4分)
h(x)max=h(1)=0…(6分)
∴a≥0,
故实数a的取值范围为[0,+∞).…(7分)
(2)g(x)=2x3+ax-2,x>0
∵g′(x)=6x2+a…(9分)
当a≥0时,g′(x)≥0恒成立,
∴g(x)在(0,+∞)单调递增,无最小值,不合题意,
∴a<0.…(11分)
令g′(x)=0,则
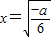 (舍负)
(舍负)∵0<x<
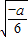 时,g′(x)<0;x>
时,g′(x)<0;x>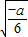 时,g′(x)>0,
时,g′(x)>0,∴g(x)在
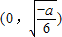 上单调递减,在
上单调递减,在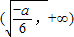 上单调递增,
上单调递增,则
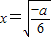 是函数的极小值点.
是函数的极小值点.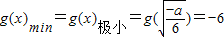 .…(13分)
.…(13分)解得a=-6,
故
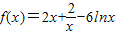 .…(14分)
.…(14分)点评:本题考查函数是增函数时实数的取值范围的求法,考查函数的解析式的求法,解题时要认真审题,仔细解答,注意导数性质的合理运用.

练习册系列答案
相关题目





 的定义域为
的定义域为 ,部分函数值如表所示,其导函数的图象如图所示,若正数
,部分函数值如表所示,其导函数的图象如图所示,若正数 ,
, 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( ) 



 B.
B. C.
C. D.
D.
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。