Question

两个袋中各装有编号为1，2，3，4的4个小球，分别从每个袋中摸出一个小球，所得两球编号数之和小于5的概率为________．

Answer 1

分析：所有的取法共有4×4=16种，分第一个袋中的球编号数为1、2、3 这三种情况，分别求出第二个袋中的球编号的情况，从而得到两球编号数之和小于5的取法种数，从而求出
所得两球编号数之和小于5的概率．
解答：所有的取法共有4×4=16种，若第一个袋中的球编号数为1，则第二个袋中的球编号数为1，2，3，有3种情况．
若第一个袋中的球编号数为2，则第二个袋中的球编号数为1，2，有2种情况．
若第一个袋中的球编号数为3，则第二个袋中的球编号数为1，有1种情况．
故所得两球编号数之和小于5的取法共有3+2+1=6种，故所得两球编号数之和小于5的概率为 =，
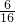故答案为 ．
点评：本题主要考查排列、组合以及简单计数原理的应用，体现了分类讨论的数学思想，属于中档题．