题目内容
设等差数列 的前
的前 项和为
项和为 ,且
,且 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前 项和为
项和为 ,且
,且 (
( 为常数),令
为常数),令 ,求数列
,求数列 的前
的前 项和
项和 。
。
【答案】
(Ⅰ) (Ⅱ)
(Ⅱ)
【解析】(Ⅰ)设等差数列 的公差为
的公差为 ,则
,则
 ,解得
,解得 ,
,
所以
(Ⅱ)由(Ⅰ)得 ,所以
,所以 .
.


当 时,
时,
因此
所以

相减得
 ,
,

化简得
【考点定位】本题从等差数列的基本问题(首项、公差、通项公式)入手,通过新数列的构造考查了 与
与 的关系、错位相减法求和等,涉及等比数列的求和公式的应用、代数式的化简等,是对运算能力的有力考查.
的关系、错位相减法求和等,涉及等比数列的求和公式的应用、代数式的化简等,是对运算能力的有力考查.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 的前
的前 项和为
项和为 且满足
且满足 则
则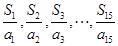 中最大的项为( )
中最大的项为( ) B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,已知
,已知 ,
, ,则
,则 .
.