Question

在平面直角坐标系xoy中，若不等式组

y≥0 y≤2x y≤k(x-1)-1

表示一个三角形区域，则实数k的取值范围是

（-∞，-1）

．

Answer 1

分析：先作出不等式对应的平面区域，利用平面区域是三角形区域，确定参数k的取值范围．

解答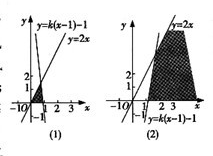：解：直线y=k（x-1）-1表示过定点（1，-1）的直线．
当这条直线的斜率为负值时，该直线与y轴的交点必须在坐标原点上方，
即直线的斜率k∈（-∞，-1）时，可构成三角形区域如题（1）．
当这条直线的斜率为正值时，y≤k（x-1）-1所表示的是直线y=k（x-1）-1及其下方的平面，
这个区域和已知区域的交集是一个无界区域，如题（2）所示，不能构成三角形，
当直线斜率为0时，构不成平面区域，因此k的取值范围是（-∞，-1）．
故答案为：（-∞，-1）．

点评：本题很容易在分析动直线的位置时出错，这个错误就是当直线y=k（x-1）-1的斜率为正值时，误以为三条直线仍然能够构成三角形．所以在画图时要注意．