Question

【题目】已知椭圆E:=1(a>b>0)过点A,离心率为,点F1,F2分别为其左、右焦点.

(1)求椭圆E的标准方程;

(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点P,Q,且?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.

Answer 1

【答案】（1）；（2）

【解析】

（1）由椭圆的离心率为可得，故椭圆的方程为，再根据点A在椭圆上得到，于是可得方程为．（2）假设满足条件的圆存在,其方程为，然后分直线PQ的斜率存在和不存在两种情况讨论可得存在满足题意得圆，其方程为；最后根据弦长公式和二次函数的知识得到|PQ|max=．

(1)由题意得e=,

所以，

故椭圆的方程为，

因为点A在椭圆上，

所以，

解得，

所以椭圆E方程为.

(2)假设满足条件的圆存在,其方程为.

①当直线PQ的斜率存在时,设直线方程为,

由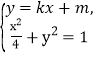消去y整理得(1+4k2)x2+8mkx+4m2-4=0,

令P(x1,y1),Q(x2,y2),

则x1+x2=-,x1x2=.

∵,

∴x1x2+y1y2=0.

∴+m2=0.

∴5m2=4k2+4.

由直线PQ与圆相切,则r2=.

所以存在圆满足题意，且圆的方程为.

②当直线PQ的斜率不存在时,也适合.

综上所述,存在圆心在原点的圆满足题意.

由弦长公式可得|PQ|=

.

又b2=k2+,

代入上式可得|PQ|=.

令4k2+1=t,即k2=,t≥1,

则|PQ|===,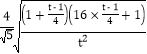

当时,即k=±时,|PQ|max=.

当直线的斜率k不存在时,|PQ|=|y1-y2|=,

综上可得|PQ|max=.