Question

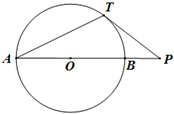
选修4-1：几何证明选讲
已知圆O直径AB=4，将线段AB延长到点P，使BP=1．作直线PT切圆O于点T．
（1）求线段PT的长；
（2）求线段AT的长．

Answer 1

分析：（1）由切割线定理，结合题中数据加以计算，即可得到线段PT的长；
（2）连接TB，得∠ATB=90°，得到AT²+BT²=AB²=16…①．由切线的性质证出△TPB∽△APT，计算出AT=

5

TB…②，两式联解即可算出线段AT的长．

解答：解：（1）由切割线定理，可得PT²=PB•PA，
∵BP=1，直径AB=4，可得AP=5
∴PT²=PB•PA=5，可得PT=

5

（舍负）．…（5分）
（2）连接TB，由AB是圆的直径，可得∠ATB=90°，
∴AT²+BT²=AB²=16…①，
∵直线PT切圆O于点T，∴∠PTB=∠PAT，
∵∠TPB=∠APT，∴△TPB∽△APT，可得

AT

TB

=

PT

PB

=

5

，
解得AT=

5

TB…②，
联解①②，可得AT=

2 30

3

．…（10分）

点评：本题给出圆的一条切线和一条直径，求证线段的长度．着重考查了圆的切线的性质、三角形相似的判定与性质等知识，属于中档题．