题目内容
集合M={y|y=|x+1|+|x-1|},N={x|y=lg(x-2)},则(CRN)∩M为( )
分析:由y=|x+1|+|x-1|≥|1+x+1-x|=2可求M,由对数函数的定义域可求N,进而可求CRN,即可求解
解答:解:由y=|x+1|+|x-1|≥|1+x+1-x|=2可知,M={y|y≥2}
由y=lg(x-2)可知x-2>0
∴N={x|y=lg(x-2)}={x|x>2},CRN={x|x≤2}
则(CRN)∩M=[2,+∞)∩(-∞,2]={2}
故选D
由y=lg(x-2)可知x-2>0
∴N={x|y=lg(x-2)}={x|x>2},CRN={x|x≤2}
则(CRN)∩M=[2,+∞)∩(-∞,2]={2}
故选D
点评:本题主要考查了绝对值不等式的性质的应用,对数函数的定义域的求解及集合的交、补集的求解,属于基础试题

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
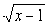 },则M∩P等于 ( )
},则M∩P等于 ( ) ,则M∩P=( )
,则M∩P=( ) },则M∩P=( )
},则M∩P=( )