题目内容
(14分)已知定义在R上函数![]() 是奇函数.
是奇函数.
(1)对于任意![]() 不等式
不等式![]() 恒成立, 求
恒成立, 求![]() 的取值范围.
的取值范围.
(2)若对于任意实数,m,x,![]() 恒成立,求t的取值范围.
恒成立,求t的取值范围.
(3)若![]() 是定义在R上周期为2的奇函数,且当
是定义在R上周期为2的奇函数,且当![]() 时,
时,![]() ,求
,求![]() 的所有解
的所有解
(1)∵![]() 为奇函数,即
为奇函数,即![]() ∴
∴![]()
![]()
∴![]() ·····(2分)
·····(2分)
易证![]() 在R上单调递减 ·····(3分)
在R上单调递减 ·····(3分)
由![]() 得
得
![]() 即
即![]() 恒成立
恒成立
又![]()
∴![]() ·····(5分)
·····(5分)
(2)由![]() 单减可知
单减可知
![]()
又![]() 恒成立
恒成立
∴只需![]() ·····(7分)
·····(7分)
即![]() 恒成立
恒成立
∴![]()
即![]() ∴
∴![]() ·····(9分)
·····(9分)
(3)∵![]() 为奇函数
为奇函数 ![]()
又![]() 的周期为
的周期为![]() ∴
∴![]()
∴![]() ·····(10分)
·····(10分)
当![]() 时
时![]() 为单调递减
为单调递减
∴![]() ·····(11分)
·····(11分)
由g(x)的周期为2,![]() 所有解为
所有解为![]() ·····(14分)
·····(14分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 上的奇函数
上的奇函数 满足
满足 ,且对任意
,且对任意 有
有 .
. ,
, ,求数列
,求数列 的通项公式.
的通项公式.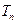 为
为 的前
的前 项和,若
项和,若 对
对 恒成立,求
恒成立,求 的最大值.
的最大值. ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值; ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.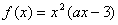 ,其中a为常数.
,其中a为常数.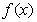 的一个极值点,求a的值;
的一个极值点,求a的值;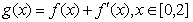 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.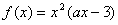 ,其中a为常数.
,其中a为常数.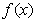 的一个极值点,求a的值;
的一个极值点,求a的值;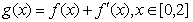 ,在x=0处取得最大值,求正数a的取值范围.
,在x=0处取得最大值,求正数a的取值范围.