题目内容
已知函数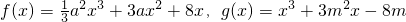 ,
,
(Ⅰ)求f(x)在x=1处的切线斜率的取值范围;
(Ⅱ)求当f(x)在x=1处的切线的斜率最小时,f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下,是否总存在实数m,使得对任意的x1∈[-1,2],总存在x0∈[0,1],使得g(x0)=f(x1)成立?若存在,求出实数m的取值范围;若不存在,说明理由.
解:(1)f′(x)=a2x2+6ax+8,f′(1)=a2+6a+8=(a+3)2-1≥-1
所以f(x)在x=1处的切线斜率的取值范围为[-1,+∞)(4分)
(2)由(1)知a=-3,则f(x)=3x3-9x2+8x(6分)
(3)f′(x)=9x2-18x+8=(3x-2)(3x-4),则有
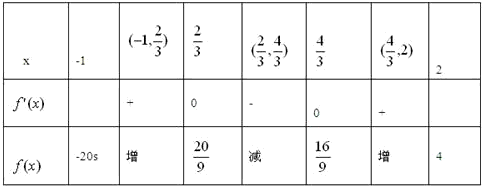 (10分)
(10分)
所以当x1∈[-1,2]时,-20≤f(x1)≤4,
假设对任意的x1∈[-1,2]都存在x0∈[0,1]使得g(x0)=f(x1)成立,
设g(x0)的最大值为T,最小值为t,则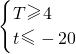 (12分)
(12分)
又g′(x)=9x2+3m2>0,所以当x0∈[0,1]时,
T=g(1)=1+3m2-8m≥4且t=g(0)=-8m≤-20,所以m≥3.(14分)
分析:(Ⅰ)先求函数的导数,在x=1处的导数就是切线斜率,再求其取值范围;
(Ⅱ)直接求当f(x)在x=1处的切线的斜率最小时,f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下,先求函数的导数,再确定单调性,是否总存在实数m,
使得对任意的x1∈[-1,2],总存在x0∈[0,1],使得g(x0)=f(x1)成立,
就是g(x0)的值域包含f(x1),求出g(x0)的最大值和最小值,再求实数m的取值范围;
点评:本题考查直线的斜率,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程,考查分析问题解决问题的能力,是中档题.
所以f(x)在x=1处的切线斜率的取值范围为[-1,+∞)(4分)
(2)由(1)知a=-3,则f(x)=3x3-9x2+8x(6分)
(3)f′(x)=9x2-18x+8=(3x-2)(3x-4),则有
 (10分)
(10分)所以当x1∈[-1,2]时,-20≤f(x1)≤4,
假设对任意的x1∈[-1,2]都存在x0∈[0,1]使得g(x0)=f(x1)成立,
设g(x0)的最大值为T,最小值为t,则
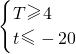 (12分)
(12分)又g′(x)=9x2+3m2>0,所以当x0∈[0,1]时,
T=g(1)=1+3m2-8m≥4且t=g(0)=-8m≤-20,所以m≥3.(14分)
分析:(Ⅰ)先求函数的导数,在x=1处的导数就是切线斜率,再求其取值范围;
(Ⅱ)直接求当f(x)在x=1处的切线的斜率最小时,f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下,先求函数的导数,再确定单调性,是否总存在实数m,
使得对任意的x1∈[-1,2],总存在x0∈[0,1],使得g(x0)=f(x1)成立,
就是g(x0)的值域包含f(x1),求出g(x0)的最大值和最小值,再求实数m的取值范围;
点评:本题考查直线的斜率,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程,考查分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目
 .
. .
. 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
.