题目内容
下列命题中,真命题是( )
分析:根据两个向量和仍然是一个向量,可以判断A的真假;根据向量数量积为0,两个向量可能垂直,可以判断B的真假;根据向量数量积公式,我们可以判断C的真假;根据数乘向量及其几何意义,可以判断D的真假;进而得到答案.
解答:解:若
与
互为负向量,则
+
=
,故A为假命题;
若
•
=0,则
=
或
=
或
⊥
,故B为假命题;
若
,
都是单位向量,则-1≤
•
≤1,故C为假命题;
若k为实数且k
=
,则k=0或
=
,故D为真命题;
故选D
| a |
| b |
| a |
| b |
| 0 |
若
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
若
| a |
| b |
| a |
| b |
若k为实数且k
| a |
| 0 |
| a |
| 0 |
故选D
点评:本题考查的知识点是向量的加法及其几何意义,向量的数乘运算及其几何意义,平面向量的数量积的运算,其中熟练掌握平面向量的基本定义,基本概念,是解答本题的关键,本题考查的点都是向量模块的易错,易忽略点,在解答向量问题时,一定要注意本题错误答案的错因.

练习册系列答案
相关题目
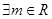 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1