题目内容
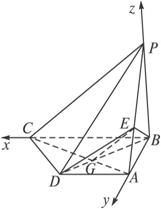
如图,四棱锥P—ABCD中,侧棱PB⊥底面ABCD,CD⊥PD.底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.点E在棱PA上,且PE=2EA.(1)求异面直线PA与CD所成的角;
(2)求二面角A-BE-D的大小(用反三角函数表示).
思路解析:本题第一问,要求异面直线所成的角,可以转而去求与这两条直线相关的向量的夹角,从而得到结果.而要求相关向量的夹角,可以考虑建立合适的坐标系,找到相关向量的坐标,从而得到结果;第二问,要求二面角的大小可以考虑去求这两个平面的法向量的夹角,从而找到结果.

解:(1)建立如图所示的直角坐标系B—xyz.设BC=a,则A(0,3,0),P(0,0,3),D(3,3,0),C(a,0,0),![]() =(3-a,3,0),
=(3-a,3,0),![]() =(3,3,-3),
=(3,3,-3),
∵CD⊥PD,
∴![]() ·
·![]() =0,即3(3-a)+9=0,a=6.
=0,即3(3-a)+9=0,a=6.
∵![]() =(-3,3,0),
=(-3,3,0),![]() =(0,3,-3),cos〈
=(0,3,-3),cos〈![]() ,
,![]() 〉=
〉=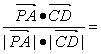
![]() ,
,
∴异面直线PA与CD所成的角是60°.
(2)设平面BED的法向量为n1=(x,y,1),∵![]() =(0,2,1),
=(0,2,1),![]() =(3,3,0),
=(3,3,0),
由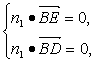 ,得
,得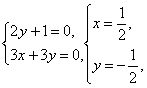 即n1=(
即n1=(![]() ,-
,-![]() ,1).
,1).
又∵平面ABE的法向量n=(1,0,0),∴cos〈n1,n2〉=![]()
因此,二面角A-BE-D的大小为arccos![]()

练习册系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=