题目内容
若集合M具有以下性质:①0∈M,1∈M;②若x、y∈M,则x-y∈M,且x≠0时,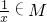 .则称集合M是“好集”.
.则称集合M是“好集”.
(Ⅰ)分别判断集合P={-1,0,1},有理数集Q是否是“好集”,并说明理由;
(Ⅱ)设集合A是“好集”,求证:若x、y∈A,则x+y∈A.
(本小题满分12分)
解:(Ⅰ)集合P不是“好集”-----------------------------
理由是:假设集合P是“好集”,因为-1∈P,1∈P,所以-1-1=-2∈P这与-2∉P矛盾---------------
有理数集Q是“好集”-------------------------------------
因为0∈Q,1∈Q,对任意的x,y∈Q,有x-y∈Q,且x≠0时, ∈Q.所以有理数集Q是“好集”----------
∈Q.所以有理数集Q是“好集”----------
(Ⅱ)因为集合A是“好集”,所以 0∈A.若x、y∈A,则0-y∈A,即-y∈A.
所以x-(-y)∈A,即x+y∈A------------------------------
分析:(I)直接利用“好集”的概念和集合P,能够推导出集合P是不是“好集”,有理数集Q是不是“好集”.
(II)集合A是“好集”,利用“好集”的概念,能够证明若-y∈A,则x-(-y)∈A,即x+y∈A.
点评:本题主要考查了元素与集合关系的判断,以及新定义的理解,同时考查了运算求解的能力,属于基础题.
解:(Ⅰ)集合P不是“好集”-----------------------------
理由是:假设集合P是“好集”,因为-1∈P,1∈P,所以-1-1=-2∈P这与-2∉P矛盾---------------
有理数集Q是“好集”-------------------------------------
因为0∈Q,1∈Q,对任意的x,y∈Q,有x-y∈Q,且x≠0时,
 ∈Q.所以有理数集Q是“好集”----------
∈Q.所以有理数集Q是“好集”----------(Ⅱ)因为集合A是“好集”,所以 0∈A.若x、y∈A,则0-y∈A,即-y∈A.
所以x-(-y)∈A,即x+y∈A------------------------------
分析:(I)直接利用“好集”的概念和集合P,能够推导出集合P是不是“好集”,有理数集Q是不是“好集”.
(II)集合A是“好集”,利用“好集”的概念,能够证明若-y∈A,则x-(-y)∈A,即x+y∈A.
点评:本题主要考查了元素与集合关系的判断,以及新定义的理解,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
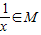 .则称集合M是“好集”.
.则称集合M是“好集”.