题目内容
 某程序流程框图如图所示,现执行该程序,输入下列函数,f(x)=sin
某程序流程框图如图所示,现执行该程序,输入下列函数,f(x)=sin| 2π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
A、f(x)=sin
| ||
B、f(x)=cos
| ||
C、f(x)=tan
| ||
| D、非上述函数 |
分析:先根据函数f(x)满足f(x)+f(-
-x)=0得到函数y=f(x)关于(-
,0)对称,再根据函数f(x)满足f(x)+f(
+x)=0得到函数y=f(x)的周期为3,最后将三个函数进行逐一进行判定即可.
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
解答:解:根据函数f(x)满足f(x)+f(-
-x)=0可知函数y=f(x)关于(-
,0)对称;
三个函数f(x)=sin
x,f(x)=cos
,f(x)=tan
x中,
f(x)=tan
x不满足f(x)+f(
+x)=0,故不合题意;
(-
,0)不是函数f(x)=sin
x的对称中心,故不合题意;
而函数f(x)=cos
关于(-
,0)对称,周期为3,满足条件
故选:B.
| 3 |
| 2 |
| 3 |
| 4 |
三个函数f(x)=sin
| 2π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
f(x)=tan
| 4π |
| 3 |
| 3 |
| 2 |
(-
| 3 |
| 4 |
| 2π |
| 3 |
而函数f(x)=cos
| 2π |
| 3 |
| 3 |
| 4 |
故选:B.
点评:本题主要考查了条件结构叠加,程序执行时需依次对“条件1”、“条件2”…都进行判断,只有遇到能满足的条件才执行该条件对应的操作,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
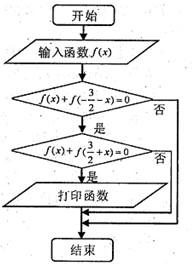 某程序流程框图如图所示,现执行该程序,输入下列函数,
某程序流程框图如图所示,现执行该程序,输入下列函数,
 则可
则可 ( )[来源:]
( )[来源:] B.
B.



 则可以输出的函数是
则可以输出的函数是 =__________
=__________


 则可以输出的函数是
则可以输出的函数是 =___________
=___________