题目内容
（本小题满分14分）
已知
中，角
的对边分别为
．
（1）证明：
；
（2）证明：不论
取何值总有
；
（3）若
，证明：
．
（本小题满分14分）
[解答]：（1）
，∴要证
，即证
，
整理得：
，即证
，而在三角形中显然成立，则原不等式成立；
（2）令
，
由余弦定理
，
，
在三角形中，
，
，
再由
得：不论
取何值总有
；
（3）
，∴
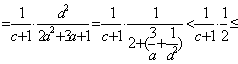
即原不等式成立．
练习册系列答案
相关题目
题目内容
（本小题满分14分）
已知中，角的对边分别为．
（1）证明：；
（2）证明：不论取何值总有；
（3）若，证明：．
（本小题满分14分）
[解答]：（1），∴要证，即证，
整理得：，即证，而在三角形中显然成立，则原不等式成立；
（2）令，
由余弦定理，
，
在三角形中，，，
再由得：不论取何值总有；
（3），∴
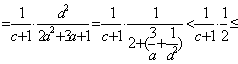
即原不等式成立．
(a＞b＞0)，曲线C2的方程为y=
，且曲线C1与C2在第一象限内只有一个公共点P。（1）试用a表示点P的坐标；（2）设A、B是椭圆C1的两个焦点，当a变化时，求△ABP的面积函数S(a)的值域；（3）记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积，试求函数f(a)=min{g(a), S(a)}的表达式。
=2，点（
）在函数
的图像上，其中
=
.
}是等比数列；
，求
及数列{
}的通项公式；
，求数列{
}的前n项和
，并证明
.
天(
)的销售价格(单位：元)为
，第
，已知该商品成本为每件25元.
关于第
的图像在点
处的切线与直线
平行.
，
满足的关系式；
上恒成立，求
（
）