题目内容
已知数列{an}的前n项和为Sn且满足an+2Sn·Sn-1=0(n≥2,n∈N*),a1=(Ⅰ)求证:数列{![]() }为等差数列;
}为等差数列;
(Ⅱ)求an的表达式.
(Ⅰ)证明:∵-an=2Sn·Sn-1,
∴-Sn+Sn-1=2Sn·Sn-1(n≥2),Sn≠0,(n=1,2,3,…)
∴![]() =2,∴{
=2,∴{![]() }成等差数列
}成等差数列
(Ⅱ)又![]() =2,
=2,
∴{![]() }=2+(n-1)·2=2n,∴Sn=
}=2+(n-1)·2=2n,∴Sn=![]()
当n≥2时,an=Sn-Sn-1=![]()
当n=1,S1=a1=![]() ,an=
,an=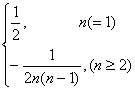 .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |