题目内容
已知F是双曲线 的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且
的左焦点,A为右顶点,上下虚轴端点B、C,若FB交CA于D,且 ,则此双曲线的离心率为( ).
,则此双曲线的离心率为( ).
A .  B.
B. C.
C.  D.
D.
B.
解析试题分析:如图,由已知可得直线FB的方程为: ,直线AC的方程为:
,直线AC的方程为: ,联立前两方程可得D点坐标为:
,联立前两方程可得D点坐标为: ,因此有
,因此有 ,又
,又 ,所以有
,所以有 ,整理得
,整理得 ,又
,又 ,所以有:
,所以有: 即
即 ,故
,故 .
.
考点:直线方程的交点问题,两点间的距离公式(或向量的模长公式),双曲线的性质(含离心率公式).

练习册系列答案
相关题目
已知抛物线关于 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点 ,若点
,若点 到该抛物线焦点的距离为3,则
到该抛物线焦点的距离为3,则 =( )
=( )
A. | B.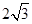 | C.4 | D. |
直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于( )
A. | B.2 | C. | D. |
已知双曲线 -
- =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
A.- =1 =1 | B. - - =1 =1 |
C. - - =1 =1 | D. - - =1 =1 |
 的准线与双曲线
的准线与双曲线 交于A,B两点,点F为抛物线的焦点,若
交于A,B两点,点F为抛物线的焦点,若 为直角三角形,则双曲线的离心率是
为直角三角形,则双曲线的离心率是

 (
( )的焦点
)的焦点 为双曲线
为双曲线 (
( )的一个焦点,经过两曲线交点的直线恰过点
)的一个焦点,经过两曲线交点的直线恰过点
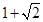


 的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ).
的焦点F,且交抛物线与A、B两点,若AB的中点到抛物线准线的距离1,则P的值为( ). C.
C. D.
D.
 ,
, 分别是双曲线
分别是双曲线 的左、右焦点,过点
的左、右焦点,过点 轴的直线与双曲线交于
轴的直线与双曲线交于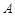 ,
, 两点,若
两点,若 是钝角三角形,则该双曲线离心率的取值范围是
是钝角三角形,则该双曲线离心率的取值范围是


