题目内容
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
(Ⅰ)求证:BM∥平面PAD;
(Ⅱ)在侧面PAD内找一点N,使MN⊥平面PBD;
(Ⅲ)求直线PC到平面PBD所成角的正弦.
解:(Ⅰ)∵M是PC的中点,取PD的中点E,则ME![]()
![]() CD,又AB
CD,又AB![]()
![]() CD
CD
∴四边形ABME为平行四边形∴BM∥24,BM![]() 平面PAD
平面PAD
EA![]() 平面PAD ∴BM∥平面PAD
平面PAD ∴BM∥平面PAD
(Ⅱ)以A为原点,以AB、AD、AP所在直线为x轴、y轴、z轴建立空间直角坐标系,如图,
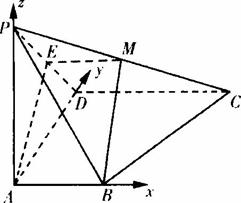
则B(1,0,0),C(2,2,0),D(0,2,0),P(0.0,2),M(1,1,1),E(0,1,1)在平面PAD内设N(0,y,z),
![]() =(-1,y-1,z-1),
=(-1,y-1,z-1),![]() =(1,0,-2),
=(1,0,-2),![]() =:(1,-2,0)
=:(1,-2,0)
由![]() ∴
∴![]() =-1-2z+2=0.∴z=
=-1-2z+2=0.∴z=![]() ;
;
由![]() ∴
∴![]() =-1-2y+2=0 ∴y=
=-1-2y+2=0 ∴y=![]()
∴N(0,![]() ,
,![]() ) ∴N是AE的中点,此时MN⊥平面PBD
) ∴N是AE的中点,此时MN⊥平面PBD
(Ⅲ)设直线PC与平面PBD所成的角为θ
![]() =(2,2,-2),
=(2,2,-2),![]() =(-1,
=(-1,![]() ),设(
),设(![]() )为α,
)为α,
cosα=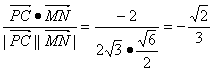 sinθ=-cosα=
sinθ=-cosα=![]()
故直线PC与平面PBD所成角的正弦为![]()
解法二:(1)∵M是PC的中点,取PD的中点E,则ME![]()
![]() CD,又AB
CD,又AB![]()
![]() CD
CD
∴四边形ABME为平行四边形∴BM∥EA,BM![]() 平面PAD
平面PAD
EA![]() 平面PAD ∴BM∥平面PAD
平面PAD ∴BM∥平面PAD

(Ⅱ)由(Ⅰ)知ABME为平行四边形PA⊥底面ABCD ∴PA⊥AB,又AB⊥AD
∴AB⊥平面PAD 同理CD⊥平面PAD,AE平面PAD∴AB⊥AE ∴ABME为矩形
CD∥ME,CD⊥PD,又PD⊥AE∴ME⊥PD ∴PD⊥平面ABME PD![]() 平面PBD
平面PBD
∴平面PBD⊥平面ABME 作MF⊥EB故MF⊥平面PBDMF交AE于N,在矩形ABME内,AB=ME=1,AE=![]() ∴MF=
∴MF=![]() ,NE=
,NE=![]() N为AE的中点
N为AE的中点
∴当点N为AE的中点时,MN⊥平面PBD
(Ⅲ)由(Ⅱ)知MF为点M到平面PBD的距离,∠MPF为直线PC与平面PBD所成的角,设为θ,sinθ=M=![]() ∴直线PC与平面PBD所成的角的正弦值为
∴直线PC与平面PBD所成的角的正弦值为![]()

 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.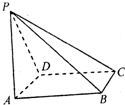 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,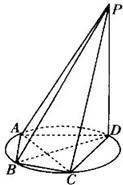 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.