题目内容
 如图,已知椭圆
如图,已知椭圆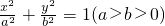 及两条直线
及两条直线 ,其中
,其中 ,且l1,l2分别交x轴于C、D两点.从l1上一点A发出一条光线经过椭圆的左焦点F被石轴反射后与l2交于点B.若AF⊥BF,且∠ABD=75°,则椭圆的离心率等于
,且l1,l2分别交x轴于C、D两点.从l1上一点A发出一条光线经过椭圆的左焦点F被石轴反射后与l2交于点B.若AF⊥BF,且∠ABD=75°,则椭圆的离心率等于
- A.A

- B.

- C.

- D.

C
分析:根据光线反射的几何性质,得∠AFC=∠AFC=45°,从而得到Rt△ACF与Rt△BDF都是等腰直角三角形.Rt△ABF中算出∠ABF=30°,得到|BF|= |AF|,从而有|DF|=
|AF|,从而有|DF|= |CF|,结合椭圆的几何性质将其转化为关于a、c的等式,化简整理即可得到该椭圆的离心率.
|CF|,结合椭圆的几何性质将其转化为关于a、c的等式,化简整理即可得到该椭圆的离心率.
解答:根据题意,得∠AFC=∠AFC= (180°-90°)=45°
(180°-90°)=45°
∴Rt△ACF与Rt△BDF都是等腰直角三角形.
∵∠ABD=75°,∴∠ABF=75°-45°=30°
Rt△ABF中,tan30°=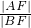 =
= ,得|BF|=
,得|BF|= |AF|
|AF|
∵|CF|= |AF|,|DF|=
|AF|,|DF|= |BF|,∴|DF|=
|BF|,∴|DF|= |CF|…(*)
|CF|…(*)
∵椭圆方程是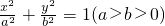 ,
,
∴左焦点F(-c,0)
因此,|DF|= +c,|CF|=
+c,|CF|= -c,代入(*)得
-c,代入(*)得
 +c=
+c= (
( -c),即(
-c),即( +1)c=(
+1)c=( -1)
-1)
∴两边都除以a,得( +1)e=(
+1)e=( -1)
-1) ,得e2=
,得e2=
∴离心率e= =
= (舍负)
(舍负)
故选:C
点评:本题给出光的反射问题,求椭圆的离心率,着重考查了椭圆的标准方程与简单几何性质和直角三角形的有关性质等知识,属于中档题.
分析:根据光线反射的几何性质,得∠AFC=∠AFC=45°,从而得到Rt△ACF与Rt△BDF都是等腰直角三角形.Rt△ABF中算出∠ABF=30°,得到|BF|=
 |AF|,从而有|DF|=
|AF|,从而有|DF|= |CF|,结合椭圆的几何性质将其转化为关于a、c的等式,化简整理即可得到该椭圆的离心率.
|CF|,结合椭圆的几何性质将其转化为关于a、c的等式,化简整理即可得到该椭圆的离心率.解答:根据题意,得∠AFC=∠AFC=
 (180°-90°)=45°
(180°-90°)=45°∴Rt△ACF与Rt△BDF都是等腰直角三角形.
∵∠ABD=75°,∴∠ABF=75°-45°=30°
Rt△ABF中,tan30°=
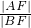 =
= ,得|BF|=
,得|BF|= |AF|
|AF|∵|CF|=
 |AF|,|DF|=
|AF|,|DF|= |BF|,∴|DF|=
|BF|,∴|DF|= |CF|…(*)
|CF|…(*)∵椭圆方程是
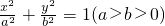 ,
,∴左焦点F(-c,0)
因此,|DF|=
 +c,|CF|=
+c,|CF|= -c,代入(*)得
-c,代入(*)得 +c=
+c= (
( -c),即(
-c),即( +1)c=(
+1)c=( -1)
-1)
∴两边都除以a,得(
 +1)e=(
+1)e=( -1)
-1) ,得e2=
,得e2=
∴离心率e=
 =
= (舍负)
(舍负)故选:C
点评:本题给出光的反射问题,求椭圆的离心率,着重考查了椭圆的标准方程与简单几何性质和直角三角形的有关性质等知识,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 如图,已知椭圆
如图,已知椭圆 及两条直线
及两条直线 ,其中
,其中 ,且l1,l2分别交x轴于C、D两点.从l1上一点A发出一条光线经过椭圆的左焦点F被石轴反射后与l2交于点B.若AF⊥BF,且∠ABD=75°,则椭圆的离心率等于( )
,且l1,l2分别交x轴于C、D两点.从l1上一点A发出一条光线经过椭圆的左焦点F被石轴反射后与l2交于点B.若AF⊥BF,且∠ABD=75°,则椭圆的离心率等于( )



