题目内容
已知向量 =(sinA,cosA+1),
=(sinA,cosA+1), =
= ,
, ∥
∥ ,且A为锐角.
,且A为锐角.
(Ⅰ)求角A的大小;
(Ⅱ)设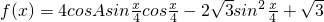 ,求f(x)的单调递增区间及函数图象的对称轴.
,求f(x)的单调递增区间及函数图象的对称轴.
解:(I)因为 ∥
∥ ,
,
所以 ,
,
即 ,
,
又因为A为锐角,
所以 .
.
(II)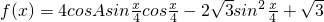
=
=
=2
令
解得
令 解得x=
解得x= ,
,
所以f(x)的单调递增区间为 ;函数图象的对称轴
;函数图象的对称轴 .
.
分析:(I)利用向量平行的充要条件得到 ,利用和角公式化简为
,利用和角公式化简为 ,求出A.
,求出A.
(II)利用三角函数的二倍角公式化简函数f(x),令 求出函数的递增区间;
求出函数的递增区间; 求出函数的对称轴.
求出函数的对称轴.
点评:解决三角函数的性质问题,应该先将三角函数化简为只含一个角一个函数,然后利用整体角处理的方法来解决.
 ∥
∥ ,
,所以
 ,
,即
 ,
,又因为A为锐角,
所以
 .
.(II)
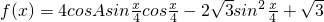
=

=

=2

令

解得

令
 解得x=
解得x= ,
,所以f(x)的单调递增区间为
 ;函数图象的对称轴
;函数图象的对称轴 .
.分析:(I)利用向量平行的充要条件得到
 ,利用和角公式化简为
,利用和角公式化简为 ,求出A.
,求出A.(II)利用三角函数的二倍角公式化简函数f(x),令
 求出函数的递增区间;
求出函数的递增区间; 求出函数的对称轴.
求出函数的对称轴.点评:解决三角函数的性质问题,应该先将三角函数化简为只含一个角一个函数,然后利用整体角处理的方法来解决.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目