题目内容

已知实数s，t满足不等式（s-t）（s+t-2）≥0．若1≤s≤4，则
t
s
的取值范围是（　　）
分析：由
(s-t)(s+t-2)≥0
1≤s≤4
可得可行域，根据
t
s
的几何意义是区域内的点与原点连线的斜率，即可求得
t
s
的取值范围．
解答：解：由
(s-t)(s+t-2)≥0
1≤s≤4
可得可行域，如图所示
∵
t
s
的几何意义是区域内的点与原点连线的斜率
∴
t
s
在直线AB位置时，取得最大值1，在点C处取得最小值
由
s=4
s+t-2=0
，可得
s=4
t=-2
，此时
t
s
取得最小值-
1
2

∴
t
s
的取值范围是[-
1
2
，1]
故选C．
点评：本题考查线性规划知识的运用，确定可行域，明确目标函数的几何意义是关键．
练习册系列答案
相关题目
定义在D上的函数，如果满足：存在常数M＞0，对任意x∈D都有|f（x）|≤M成立，则称f（x）是D上的有界函数．
（1）试判断函数f(x)=2sin(x+
π
6
)+3在实数集R上，函数g(x)=x3+
3
x
在[
1
3
，3]上是不是有界函数？若是，请给出证明；若不是，请说出理由．
（2）若已知某质点的运动距离S与时间t的关系为S(t)=
1
4
t4+3lnt-at，要使在t∈[
1
3
，3]上每一时刻的瞬时速度的绝对值都不大于13，求实数a的取值范围．
已知A、B分别是x轴和y轴上的两个动点，满足|AB|=2，点P在线段AB上，且
AP
=t
PB
（t是不为0的常数），设点P的轨迹方程为C．
（Ⅰ）求点P的轨迹方程C；
（Ⅱ）若曲线C为焦点在x轴上的椭圆，试求实数t的取值范围；
（Ⅲ）若t=2，点M、N是C上关于原点对称的两个动点，点Q的坐标为(
3
2
，3)，求△QMN的面积S的最大值．
已知圆C的方程为x2+y2=4，动点P满足：过点P作直线与圆C相交所得的所有弦中，弦长最小的为2，记所有满足条件的点P形成的几何图形为曲线M．
（1）写出曲线M所对应的方程；（不需要解答过程）
（2）过点S（0，2）的直线l与圆C交于A，B两点，与曲线M交于E，F两点，若AB=2EF，求直线l的方程；
（3）设点T（x0，y0）．
①当y0=0时，若过点T存在一对互相垂直的直线同时与圆C有两个公共点，求实数x0的取值范围；
②若过点T存在一对互相垂直的直线同时与圆C有两个公共点，试探求实数x0，y0应满足的条件．
（2013•杨浦区一模）设数列{xn}满足xn≠1且（n∈N*），前n项和为Sn．已知点p1（x1，S1），P2（x2，s2），…Pn（xn，sn）都在直线y=kx+b上（其中常数b，k且k≠1，b≠0），又yn=log
12
 xn．
（1）求证：数列{xn]是等比数列；
（2）若yn=18-3n，求实数k，b的值；
（3）如果存在t、s∈N*，s≠t使得点（t，yt）和点（s，yt）都在直线y=2x+1上．问是否存在正整数M，当n＞M时，xn＞1恒成立？若存在，求出M的最小值，若不存在，请说明理由．
定义在D上的函数，如果满足：存在常数M＞0，对任意x∈D都有|f（x）|≤M成立，则称f（x）是D上的有界函数．
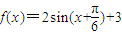（1）试判断函数在实数集R上，函数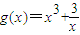在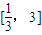上是不是有界函数？若是，请给出证明；若不是，请说出理由．
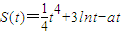（2）若已知某质点的运动距离S与时间t的关系为，要使在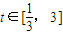上每一时刻的瞬时速度的绝对值都不大于13，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网