题目内容
对于以下四个命题:①若函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,则loga2<0;
②设函数
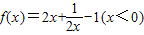 ,则函数f(x)有最小值1;
,则函数f(x)有最小值1;③函数y=(sinx+cosx)2-1的最小正周期是2π.
其中正确命题的序号是 .
【答案】分析:①利用对数函数的单调性即可判断出是否正确;
②利用基本不等式的性质和不等式的基本性质即可得出结论;
③利用平方关系和倍角公式进行化简,再利用三角函数的周期公式即可求出周期,进而判断出结论.
解答:解:①∵函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,∴0<a<1,∴loga2<loga1=0,故①正确;
②∵函数 ,∴f(x)=-
,∴f(x)=-
 -1=-3,当且仅当
-1=-3,当且仅当 时取等号,故函数f(x)有最大值,而无最小值;
时取等号,故函数f(x)有最大值,而无最小值;
③函数y=(sinx+cosx)2-1=sin2x,∴函数周期T= ,故③不正确.
,故③不正确.
故答案为①
点评:熟练掌握函数的单调性、基本不等式的性质和三角函数的周期性是解题的关键.
②利用基本不等式的性质和不等式的基本性质即可得出结论;
③利用平方关系和倍角公式进行化简,再利用三角函数的周期公式即可求出周期,进而判断出结论.
解答:解:①∵函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,∴0<a<1,∴loga2<loga1=0,故①正确;
②∵函数
 ,∴f(x)=-
,∴f(x)=-
 -1=-3,当且仅当
-1=-3,当且仅当 时取等号,故函数f(x)有最大值,而无最小值;
时取等号,故函数f(x)有最大值,而无最小值;③函数y=(sinx+cosx)2-1=sin2x,∴函数周期T=
 ,故③不正确.
,故③不正确.故答案为①
点评:熟练掌握函数的单调性、基本不等式的性质和三角函数的周期性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
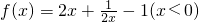 ,则函数f(x)有最小值1;
,则函数f(x)有最小值1;