题目内容
已知x≥-10，关于x的不等式|x-3|-|2x+10|+x+15-2|a+13|≥0的解集不是空集，则实数a的取值范围 ．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：问题等价于存在x≥-10使2|a+13|≤|x-3|-|2x+10|+x+15成立，化为分段函数可求出y=|x-3|-|2x+10|+x+15，x≥-10的最大值，可得a的不等式，解不等式可得．
解答：
解：关于x的不等式|x-3|-|2x+10|+x+15-2|a+13|≥0的解集不是空集
等价于存在x≥-10使2|a+13|≤|x-3|-|2x+10|+x+15成立，
故只需求出函数y=|x-3|-|2x+10|+x+15，x≥-10的最大值即可，
去绝对值可得y=
，
易得当x=-5时，函数y取最大值18，
∴只需2|a+13|≤18，解得-22≤a≤-4
故答案为：[-22，-4]
等价于存在x≥-10使2|a+13|≤|x-3|-|2x+10|+x+15成立，
故只需求出函数y=|x-3|-|2x+10|+x+15，x≥-10的最大值即可，
去绝对值可得y=
|
易得当x=-5时，函数y取最大值18，
∴只需2|a+13|≤18，解得-22≤a≤-4
故答案为：[-22，-4]
点评：本题考查绝对值不等式，转化为求函数的最值是解决问题的关键，属中档题．
练习册系列答案
相关题目
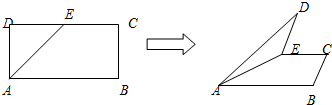
如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．PD=AD如图，在矩形ABCD中，AB=4，BC=3，E为DC边的中点，沿AE将AD折起，使二面角D-AE-B为60°，则异面直线BC与AD所成的角余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
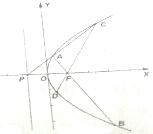如图，已知F是抛物线y2=4x的焦点，P是抛物线的准线与x轴的交点，过P作直线l交抛物线于不同的两点A、C，点B、D在抛物线上，且