题目内容
如图,在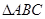 中,
中, ,
,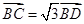 , A
, A ,则
,则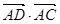 的值为( ) B D C
的值为( ) B D C
A.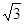 | B.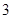 | C.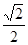 | D.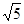 |

A
解析考点:平面向量数量积的运算.
分析:由AD⊥AB,知cos<  ,
, >=cos∠ADB=
>=cos∠ADB= 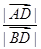 ,由
,由 =
= 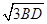 ,|
,|  |=1,知
|=1,知 ?
?  =(
=( +
+  )?
)?  =
=  ?
?  +
+  ?
?  =
=  ?
?  =
= 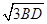 ?
?  =
=  ?|
?|  |2,由此能求出其结果.
|2,由此能求出其结果.
解:∵AD⊥AB,
∴ ?
? =0.
=0.
∴cos< ,
, >=cos∠ADB=
>=cos∠ADB=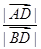 ,
,
∵ =
=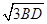 ,|
,| |=1,
|=1,
∴ ?
? 
=( +
+  )?
)? 
= ?
?  +
+  ?
? 
= ?
? 
=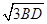 ?
? 
= ?|
?| |×|
|×| |×cos<
|×cos< ,
, >
>
= ?|
?| |×|
|×| |×
|×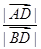
= ?||
?|| |2
|2
= ×12
×12
= .
.
故选A.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
抛物线y =4x的焦点坐标为
=4x的焦点坐标为
| A.(2,0) | B.(1,0) | C.(0,-4) | D.(-2,0) |
已知点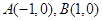 及抛物线
及抛物线 ,若抛物线上点
,若抛物线上点 满足
满足 ,则
,则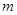 的最大值为( )
的最大值为( )
A. | B. | C. | D.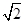 |
两个正数 的等差中项是
的等差中项是 一个等比中项是
一个等比中项是 则双曲线
则双曲线 的离心率
的离心率 等于
等于
A. | B. | C. | D. |
渐近线是 和
和 且过点
且过点 ,则双曲线的标准方程是( )
,则双曲线的标准方程是( )
A. | B. | C.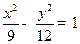 | D. |
若椭圆 的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|·|PF2|的值为( )
的共同焦点为F1,F2,P是两曲线的一个交点,则|PF1|·|PF2|的值为( )
A. | B.84 | C.3 | D.21 |
 ,过其右焦点且垂直于实轴的直线与双曲线交于M、N两点,O是坐标原点.若
,过其右焦点且垂直于实轴的直线与双曲线交于M、N两点,O是坐标原点.若 ,则双曲线的离心率为 ( ).
,则双曲线的离心率为 ( ).



 的两焦点,以线段F1F2为边作
的两焦点,以线段F1F2为边作

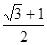

 共焦点,且一条渐近线方程是
共焦点,且一条渐近线方程是 ,则此双曲
,则此双曲 B.
B.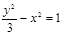 C.
C. D.
D.