题目内容
已知f(x)=(Ⅰ)证明数列{![]() }是等比数列;
}是等比数列;
(Ⅱ)令bn=![]() -2, Sn为{bn}的前n项和,求使Sn>
-2, Sn为{bn}的前n项和,求使Sn>![]() 成立的最小n值.
成立的最小n值.
解:(Ⅰ)∵![]() =2anf(an)=2an·
=2anf(an)=2an·![]() ,
,
∴![]() (5分) ∴
(5分) ∴![]() ,
,
∴数列{![]() -2}是以2为首项,
-2}是以2为首项,![]() 为公比的等比数列
为公比的等比数列
(Ⅱ)∵bn=![]() -2=(
-2=(![]() )n-2,
)n-2,
∴Sn=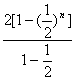 =4[1-(
=4[1-(![]() )n]
)n]
又Sn>![]() 即4[1-(
即4[1-(![]() )n]>
)n]>![]() ,∴(
,∴(![]() )n<
)n<![]()
∴n>5,∴满足Sn>![]() 的最小n为6.
的最小n为6.

练习册系列答案
相关题目
题目内容
已知f(x)=(Ⅰ)证明数列{![]() }是等比数列;
}是等比数列;
(Ⅱ)令bn=![]() -2, Sn为{bn}的前n项和,求使Sn>
-2, Sn为{bn}的前n项和,求使Sn>![]() 成立的最小n值.
成立的最小n值.
解:(Ⅰ)∵![]() =2anf(an)=2an·
=2anf(an)=2an·![]() ,
,
∴![]() (5分) ∴
(5分) ∴![]() ,
,
∴数列{![]() -2}是以2为首项,
-2}是以2为首项,![]() 为公比的等比数列
为公比的等比数列
(Ⅱ)∵bn=![]() -2=(
-2=(![]() )n-2,
)n-2,
∴Sn=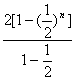 =4[1-(
=4[1-(![]() )n]
)n]
又Sn>![]() 即4[1-(
即4[1-(![]() )n]>
)n]>![]() ,∴(
,∴(![]() )n<
)n<![]()
∴n>5,∴满足Sn>![]() 的最小n为6.
的最小n为6.
