题目内容
从极点O作圆C：ρ=8cosθ的弦ON，求ON的中点M的轨迹方程.
解析:在直角坐标系中,求曲线的轨迹方程的方法有直接法、定义法、转移法,在极坐标系中,求曲线的极坐标方程这几种方法仍然是适用的.
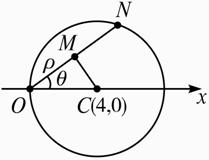
解法一:如图,圆C的圆心C(4,0),半径r=|OC|=4,连结CM.?
∵M为弦ON的中点,?
∴CM⊥ON.故M在以OC为直径的圆上.?
所以,动点M的轨迹方程是ρ=4cosθ.
解法二:解法一是定义法,下面我们用转移法来解决这个问题.?
设M点的坐标是(ρ,θ),N(ρ1,θ1).?
N点在圆ρ=8cosθ上,?
∴ρ1=8cosθ1.(*)?
∵M是ON的中点,?
∴
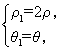将它代入(*)式得2ρ=8cosθ,故M的轨迹方程是ρ=4cosθ.
练习册系列答案
相关题目
在A、B、C、D四小题中只能选做2题，每小题10分，共计20分，请在答题纸指定区域内作答，解答应写出文字说明、证明过程或演算步骤．