题目内容
过正方体ABCD-A1B1C1D1的对角线BD1的平面与平面A1B1C1D1所成的二面角的正弦值的取值范围是分析:因为在正方体中,所以此题我们可以考虑两种极端情况:
1、当过BD1的平面为平面BB1D1D时,此时平面BB1D1D⊥平面A1B1C1D1,则二面角为
,所以正弦值为1;
2、当过BD1的平面与面BB1D1D垂直时,二面角平面角最小,为∠BD1B1,所以正弦值为
.
1、当过BD1的平面为平面BB1D1D时,此时平面BB1D1D⊥平面A1B1C1D1,则二面角为
| π |
| 2 |
2、当过BD1的平面与面BB1D1D垂直时,二面角平面角最小,为∠BD1B1,所以正弦值为
| ||
| 3 |
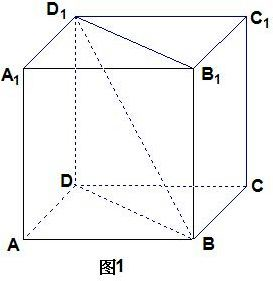
解答:解:如图1所示:当过BD1的平面为平面BB1D1D时,
∵平面BB1D1D⊥平面A1B1C1D1,
∴此时二面角最大,二面角为
,
∴正弦值为1,即为最大值;
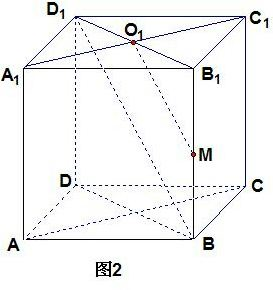
如图2所示:当过BD1的平面与面BB1D1D垂直时,二面角平面角最小,
∵平面A1ACC1⊥平面BB1D1D,
∴过BD1的平面且与平面BB1D1D垂直的平面与平面A1ACC1平行,
∴所求二面角的平面角即可看成是平面A1ACC1与平面A1B1C1D1所成的二面角的平面角,
即∠MO1B1=∠BD1B1
∴tan∠BD1B1=tan∠MO1B1=
,
∴正弦值为
,即为最小值.
故答案为:[
,1]
∵平面BB1D1D⊥平面A1B1C1D1,
∴此时二面角最大,二面角为
| π |
| 2 |
∴正弦值为1,即为最大值;
如图2所示:当过BD1的平面与面BB1D1D垂直时,二面角平面角最小,
∵平面A1ACC1⊥平面BB1D1D,
∴过BD1的平面且与平面BB1D1D垂直的平面与平面A1ACC1平行,
∴所求二面角的平面角即可看成是平面A1ACC1与平面A1B1C1D1所成的二面角的平面角,
即∠MO1B1=∠BD1B1
∴tan∠BD1B1=tan∠MO1B1=
| ||
| 3 |
∴正弦值为
| ||
| 3 |
故答案为:[
| ||
| 3 |


点评:本小题主要考查空间线面关系、二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
 如图所示,正方体ABCD-A'B'C'D'的棱长为1,E,F分别是棱AA',CC'的中点,过直线E,F的平面分别与棱BB'、DD'交于M,N,设BM=x,x∈[0,1],给出以下四个命题:
如图所示,正方体ABCD-A'B'C'D'的棱长为1,E,F分别是棱AA',CC'的中点,过直线E,F的平面分别与棱BB'、DD'交于M,N,设BM=x,x∈[0,1],给出以下四个命题: 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F 分别是棱AA',CC'的中点,过直线E、F的平面分别与棱BB′,DD′交于M、N,设BM=x,x∈[0,1],给出以下四个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E、F 分别是棱AA',CC'的中点,过直线E、F的平面分别与棱BB′,DD′交于M、N,设BM=x,x∈[0,1],给出以下四个命题: