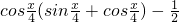题目内容
设函数y=f(x)满足f(2+x)=f(2-x),又f(x)在[2,+∞)是减函数,且f(a)≥f(0),则实数a的取值范围是
- A.a≥2
- B.a<0
- C.0≤a≤4
- D.a<0或a≥4
C
分析:先根据函数y=f(x)满足f(2+x)=f(2-x),得到函数y=f(x)的对称轴为x=2,然后根据对称性判定函数在在(-∞,2)上的单调性,最后根据单调性可求出a的范围.
解答:∵函数y=f(x)满足f(2+x)=f(2-x),
∴函数y=f(x)的对称轴为x=2
∵f(x)在[2,+∞)是减函数
∴f(x)在(-∞,2)是增函数
但a∈(-∞,2)时,f(a)≥f(0),则0≤a<2
当a∈[2,+∞)时,f(a)≥f(0)=f(4),则2≤a≤4
∴实数a的取值范围是0≤a≤4
故选C.
点评:本题主要考查了抽象函数的单调性和对称性,同时考查了转化的思想,属于中档题.
分析:先根据函数y=f(x)满足f(2+x)=f(2-x),得到函数y=f(x)的对称轴为x=2,然后根据对称性判定函数在在(-∞,2)上的单调性,最后根据单调性可求出a的范围.
解答:∵函数y=f(x)满足f(2+x)=f(2-x),
∴函数y=f(x)的对称轴为x=2
∵f(x)在[2,+∞)是减函数
∴f(x)在(-∞,2)是增函数
但a∈(-∞,2)时,f(a)≥f(0),则0≤a<2
当a∈[2,+∞)时,f(a)≥f(0)=f(4),则2≤a≤4
∴实数a的取值范围是0≤a≤4
故选C.
点评:本题主要考查了抽象函数的单调性和对称性,同时考查了转化的思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目