Question

已知函数f（x）=1+

x-|x|

4

（Ⅰ）用分段函数的形式表示函数f（x）；
（Ⅱ）在坐标系中画出函数f（x）的图象；
（Ⅲ）在同一坐标系中，再画出函数g（x）=

1

x

(x＞0)的图象（不用列表），观察图象直接写出当x＞0时，不等式f（x）＞

1

x

的解集．

Answer 1

分析：（Ⅰ）已知函数f（x）=1+

x-|x|

4

，首先要去掉绝对值，讨论x与0的关系，从而进行求解；
（Ⅱ）根据f（x）的解析式，可以画出f（x）的图象；
（Ⅲ）由第二问的图象再画出g（x）的图象，可以直接看出不等式的解集；

解答：解：（Ⅰ）因为当x≥0时，f（x）=1；                     …（2分）
当x＜0时，f（x）=

1

2

x+1；                         …（4分）
所以f（x）=

1 (x≥0) 1 2 x+1(x＜0)

；                            …（6分）
（Ⅱ）函数图象如图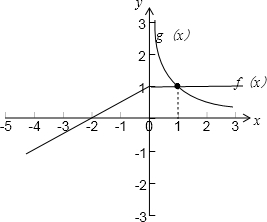：                        …（10分）

（Ⅲ）由上图可知当x＞1时，f（x）＞g（x），
∴不等式f（x）＞

1

x

的解集为{x|x＞1}                         …（13分）

点评：此题主要考查分段函数的性质，以及数形结合的方法求解不等式的解集问题，是一道基础题；