题目内容
设正四面体中,第一个球是它的内切球,第二个球是它的外接球,求这两个球的表面积之比及体积之比.
思路解析:注意到内切球球心到各面距离相等,可以得到内切球半径与正四面体棱长的关系.同样地,由外接球球心到正四面体各顶点距离相等,可以得到外接球半径与正四面体棱长的关系,从而得到它们间的表面积比及体积比.
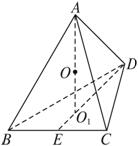
解:如图,正四面体ABCD的中心为O,△BCD的中心为O1,则第一个球半径为正四面体的中心到各面的距离,第二个球的半径为正四面体中心到顶点的距离.
设OO1=r,OA=R,正四面体的一个面的面积为S.
依题意得VA—BCD=![]() S(R+r),
S(R+r),
又VA—BCD=4VO—BCD=4×![]() r·S,∴R+r=4r,即R=3r.
r·S,∴R+r=4r,即R=3r.
∴![]()
方法归纳 正四面体与球的接切问题,可通过线面关系证出,内切球和外接球的两个球心是重合的,为正四面体高的四等分点.

练习册系列答案
相关题目
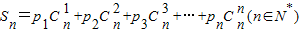 ,试求Sn(用含n的式子表示).
,试求Sn(用含n的式子表示).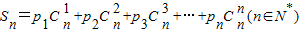 ,试求Sn(用含n的式子表示).
,试求Sn(用含n的式子表示).