题目内容
“a≥0”是“函数 在区间(-∞,0)内单调递减”的( )
在区间(-∞,0)内单调递减”的( )
| A.充要条件 | B.必要不充分条件 |
C.充分不 必要条件 必要条件 | D.即不充分也不必要条件 |
A
解析试题分析:令t=(ax-1)x=ax2-x,则 ,设
,设 =0,解得x=
=0,解得x= ,所以,当a≥0时,函数t=(ax-1)x在(-∞,
,所以,当a≥0时,函数t=(ax-1)x在(-∞, )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数,即极小值为-
,+∞)上是增函数,即极小值为- ,当x<0时,t>0,所以a≥0时,函数
,当x<0时,t>0,所以a≥0时,函数 在区间(-∞,0)内单调递减;若函数
在区间(-∞,0)内单调递减;若函数 在区间(-∞,0)内单调递减,则x
在区间(-∞,0)内单调递减,则x 时,
时,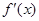 <0,即
<0,即 成立,所以2a ≥0,故选A.
成立,所以2a ≥0,故选A.
考点:1.导数的应用;2.充分必要条件的判断.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“所有能被2整除的整数都是偶数”的否定是 ( )
| A.所有不能被2整除的整数都是偶数 |
| B.所有能被2整除的整数都不是偶数 |
| C.存在一个不能被2整除的整数是偶数 |
| D.存在一个能被2整除的整数不是偶数 |
若命题p: ,则该命题的否定是( )
,则该命题的否定是( )
A. | B. |
C. | D. |
已知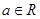 ,则“
,则“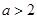 ”是“
”是“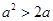 ”成立的 ( )
”成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列说法错误的是( )
A.命题“若 ”的逆否命题为:“若 ”的逆否命题为:“若 则 则 ” ” |
B.命题 则 则 |
C.若 则“ 则“ ”是“ ”是“ ”的充要条件 ”的充要条件 |
D.若“ ” 为假命题,则 ” 为假命题,则 至少有一个为假命题 至少有一个为假命题 |
已知命题p:在△ABC中,“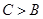 ”是“
”是“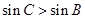 ”的充分不必要条件;命题q:“
”的充分不必要条件;命题q:“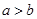 ”是“
”是“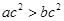 ”的充分不必要条件,则下列选项中正确的是( )
”的充分不必要条件,则下列选项中正确的是( )
| A.p真q假 | B.p假q真 | C.“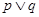 ”为假 ”为假 | D.“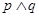 ”为真 ”为真 |
已知“ ”是“
”是“ ”的充分不必要条件,则k的取值范围是( )
”的充分不必要条件,则k的取值范围是( )
A.[2,+ ) ) | B.[1,+ ) ) | C.(2,+ ) ) | D.(一 ,-1] ,-1] |
若命题 :
: ,
, :方程
:方程 表示双曲线,则
表示双曲线,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |