Question

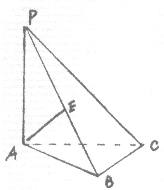如图2所示，空间几何体P-ABC中PA⊥平面ABC，AB⊥BC．PB、PC与平面ABC所成的角分别为60°和45°．AE⊥PB于E．
（1）求证：AE⊥PC；
（2）求AC与平面PBC所成的角；
（3）求AC与PB所成的角．

Answer 1

分析：（1）先根据条件得到BC⊥平面PAB，进而可得结论；
（2）先结合第一问的结论得到AE⊥面PBC，进而得∠ACE为AC与平面PBC所成角；然后通过求三角形的边长即可求出∠ACE得到结论．
（3）过B作BN

∥ .

.

AC，连AN、PN，得∠PBN等于AC与PB所成角（或补角）；然后通过求三角形的边长即可求出结论．

解答：解：如图，（1）PA⊥平面ABC⇒

PA⊥BC AB⊥BC

⇒BC⊥平面PAB⇒BC⊥AE
（2）连EC．
∵BC⊥AE，AE⊥PB于E
∴AE⊥面PBC
∴∠ACE为AC与平面PBC所成角．
设AC=a，由条件⇒PA=a，AB=

3

3

a，⇒AE=

a

2

∴sin∠ACE=

AE

AC

=

1

2

即∠ACE=30°．
∴AC与平面PBC所成角为30°．
（3）过B作BN

∥ .

.

AC，连AN、PN，
则∠PBN等于AC与PB所成角（或补角）．
由已知，设AC=a，则BN=a，PB=

2 3

3

a，PN=

AN2+PA2

=

15

3

a．
则cos∠PBN=

BN2+PB2-PN2

2•BN•PB

=

3

6

．
∵AC、PB为异面直线
∴AC、PB所成角为arccos

3

6

．

点评：本题考查直线与平面垂直、直线和平面所成的角、二面角等基础知识．考查空间想象能力、记忆能力和推理论证能力．