题目内容
已知函数![]() 的定义域是
的定义域是![]() 且
且
![]() ,
,![]() ,当
,当![]() 时,
时,![]() .
.
(1)求证:![]() 是奇函数;
是奇函数;
(2)求![]() 在区间
在区间![]()
![]() )上的解析式;
)上的解析式;
(3)是否存在正整数![]() ,使得当x∈
,使得当x∈![]() 时,不等式
时,不等式![]() 有解?证明你的结论.
有解?证明你的结论.
(1)证明略 (2)![]() (3)不存在
(3)不存在
解析:
(1) 由![]() 得
得![]() , ------------3分
, ------------3分
由![]() 得
得![]() , -----------4分
, -----------4分
故![]() 是奇函数. --------5分
是奇函数. --------5分
(2)当x∈![]() 时,
时,![]() ,
,![]() 。 ----------7分
。 ----------7分
而![]() ,
,![]() 。 ---------9分
。 ---------9分
当x∈![]() Z)时,
Z)时,![]() ,
,![]() ,
,
因此![]() 。 -------------11分
。 -------------11分
(3)不等式![]() 即为
即为![]() ,
,
即![]() 。 ---------13分
。 ---------13分
令![]() ,对称轴为
,对称轴为![]() ,
,
因此函数![]() 在
在![]() 上单调递增。------------15分
上单调递增。------------15分
因为![]() ,又
,又![]() 为正整数,
为正整数,
所以![]() ,因此
,因此![]() 在
在![]() 上恒成立,-----17分
上恒成立,-----17分
因此不存在正整数![]() 使不等式有解。 --------------18分
使不等式有解。 --------------18分

练习册系列答案
相关题目
 的定义域为
的定义域为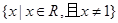 , 且
, 且 奇函数.当
奇函数.当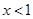 时,
时, 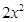 -
-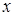 -1,那么函数
-1,那么函数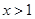 时,
时, 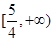 B.
B. C.
C. D.
D.
 的定义域是
的定义域是 ,函数
,函数 在
在 上的值域为
上的值域为 ,全集为
,全集为 ,且
,且 求实数
求实数 的取值范围。
的取值范围。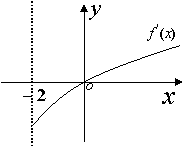 已知函数
已知函数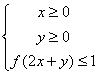 所围成的平面区域的面积是
所围成的平面区域的面积是