题目内容
直角坐标系中,抛物线x2=-3y经过伸缩变换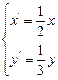 后得曲线( )
后得曲线( )
| A.y′2=-4x′ | B.x′2=-4y′ |
| C.y′2=-x′ | D.x′2=-y′ |
D
解析

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
已知函数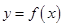 的大致图象如图所示,则函数
的大致图象如图所示,则函数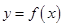 的解析式应为
的解析式应为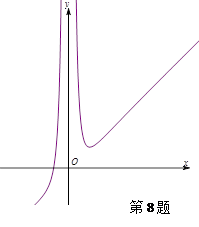
A.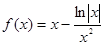 | B.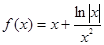 |
C.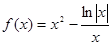 | D.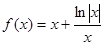 |
已知双曲线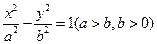 的离心率为
的离心率为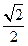 ,则椭圆
,则椭圆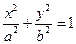 的离心率为
的离心率为
A.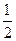 | B.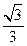 | C. | D.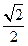 |
设双曲线 的渐近线与抛物线
的渐近线与抛物线 有且只有两个公共点,则该双曲线的离心率
有且只有两个公共点,则该双曲线的离心率
| A.5 | B. | C. | D. |
.已知双曲线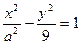
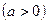 右焦点与抛物线
右焦点与抛物线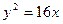 的焦点重合,则该双曲线的离心率等于
的焦点重合,则该双曲线的离心率等于
A.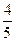 | B. | C.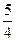 | D.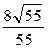 |
 的焦点
的焦点 为双曲线
为双曲线 的一个焦点,经过两曲线交点的直线恰过点
的一个焦点,经过两曲线交点的直线恰过点




 的曲线大致是 ( )
的曲线大致是 ( )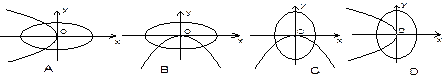
 B
B  C.
C.  D
D 

 为中心在原点焦点在
为中心在原点焦点在 的椭圆
的椭圆 的左、右焦点,抛物线
的左、右焦点,抛物线 以
以 为顶点,
为顶点, 为焦点,设
为焦点,设 为椭圆与抛物线的一个交点,如果椭圆的离心率为
为椭圆与抛物线的一个交点,如果椭圆的离心率为 ,且
,且 ,则
,则







