题目内容
已知P为双曲线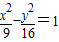
上一点，F1，F2为该双曲线的左、右焦点，若
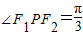，则△F1PF2的面积为 ．
【答案】分析：由P为双曲线
上一点，
，利用双曲线第一定义和余弦定理列出方程组，求出|PF1|•|PF2|=64，由此能够求出△F1PF2的面积．
解答：解：∵P为双曲线
上一点，
，
∴
，
∴
，
解得|PF1|•|PF2|=64，
∴△F1PF2的面积S=
×|PF1|•|PF2|×sin60°=
64×
=16
．
故答案为：16
．
点评：本题考查三角形的面积的求法，具本涉及到椭圆的简单性质，余弦定理，正弦定理，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．
上一点，，利用双曲线第一定义和余弦定理列出方程组，求出|PF1|•|PF2|=64，由此能够求出△F1PF2的面积．解答：解：∵P为双曲线
上一点，，∴
，∴
，解得|PF1|•|PF2|=64，
∴△F1PF2的面积S=
×|PF1|•|PF2|×sin60°=64×=16．故答案为：16
．点评：本题考查三角形的面积的求法，具本涉及到椭圆的简单性质，余弦定理，正弦定理，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
上一点，双曲线的一条渐近线方程为3x-2y=0,F1 、F2分别是双曲线的左、右焦点，若|P F1 |=3，则|P F2|=
（ ）
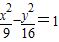上一点，F1，F2为该双曲线的左、右焦点，若
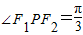，则△F1PF2的面积为 ．
上一点，双曲线的一条渐近线方程为
，
分别是双曲线的左右焦点，若，则
等于
上一点，双曲线的一条渐近线方程为
，F1,F2分别是双曲线的左右焦点，若|PF1|=5，则|PF2|等于( )