题目内容
【题目】已知函数![]() (
(![]() ,且
,且![]() ).
).
(1)当![]() 时,设集合
时,设集合![]() ,求集合
,求集合![]() ;
;
(2)在(1)的条件下,若![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,存在
,存在![]() ,使不等式
,使不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() .
.
【解析】试题分析:(1)将![]() 代入,解对数不等式即可求出;(2)化简不等式,可得
代入,解对数不等式即可求出;(2)化简不等式,可得![]() ,即
,即![]() ,再结合
,再结合![]() ,列出不等式组即可求解;(3)原问题等价于当
,列出不等式组即可求解;(3)原问题等价于当![]() 时,
时, ![]() ,分别根据增减性求出两个函数的最小值即可建立不等式
,分别根据增减性求出两个函数的最小值即可建立不等式![]() ,解不等式即可求出
,解不等式即可求出![]() 的取值范围.
的取值范围.
试题解析:
(1)由![]() 时,由
时,由![]() 得
得![]() ,即
,即![]() ,解得
,解得
![]() ,所以
,所以![]() .
.
(2)由![]() 得
得![]() ,所以
,所以![]() 可转化为;
可转化为; 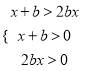 在
在![]() 上恒成立,解得实数
上恒成立,解得实数![]() 的取值范围为
的取值范围为![]() .
.
(3)对任意的![]() ,存在
,存在![]() ,使不等式
,使不等式![]() 恒成立,等价于
恒成立,等价于
![]() 时,
时, ![]() .
.
当![]() 时,由复合函数的单调性可知
时,由复合函数的单调性可知![]() 为
为![]() 上的减函数,
上的减函数, ![]() 为
为![]() 上的增函数,
上的增函数, ![]() 等价于
等价于![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,
时, ![]() 为
为![]() 上的增函数,
上的增函数, ![]() 为
为![]() 上的减函数,
上的减函数, ![]() 等价于
等价于![]() ,即
,即![]() ,解得
,解得![]() .
.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目