题目内容
数列{an}满足 ,则{an}的前40项和为________.
,则{an}的前40项和为________.
420
分析:利用数列递推式,可得数列{an}是从第一项开始,依次取2个相邻奇数项的和都等于1,从第二项开始,依次取2个相邻偶数项的和构成以5为首项,以8为公差的等差数列,由此可得结论.
解答:∵ ,
,
∴a2-a1=1,a3+a2=2,a4-a3=3,a5+a4=4,…,a50-a49=49.
∴a3+a1=1,a4+a2=5,a7+a5=1,a8+a6=13,a9+a11=1,a12+a10=21,…
从第一项开始,依次取2个相邻奇数项的和都等于1,从第二项开始,依次取2个相邻偶数项的和构成以5为首项,以8为公差的等差数列.
所以{an}的前40项和为10×1+10×5+ =420
=420
故答案为:420.
点评:本题考查数列递推式,考查数列求和,属于中档题.
分析:利用数列递推式,可得数列{an}是从第一项开始,依次取2个相邻奇数项的和都等于1,从第二项开始,依次取2个相邻偶数项的和构成以5为首项,以8为公差的等差数列,由此可得结论.
解答:∵
 ,
,∴a2-a1=1,a3+a2=2,a4-a3=3,a5+a4=4,…,a50-a49=49.
∴a3+a1=1,a4+a2=5,a7+a5=1,a8+a6=13,a9+a11=1,a12+a10=21,…
从第一项开始,依次取2个相邻奇数项的和都等于1,从第二项开始,依次取2个相邻偶数项的和构成以5为首项,以8为公差的等差数列.
所以{an}的前40项和为10×1+10×5+
 =420
=420故答案为:420.
点评:本题考查数列递推式,考查数列求和,属于中档题.

练习册系列答案
相关题目
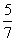 若
若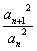 N*),则称{an}为“等方比数列”.
N*),则称{an}为“等方比数列”.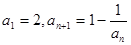 ,则a2007的值 ( )
,则a2007的值 ( )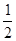 D.2
D.2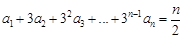 ,则
,则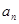 = .
= .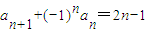 ,则{an}的前60项和为 .
,则{an}的前60项和为 .