题目内容

已知函数f(x)=,

(1)求f(x)单调递增和递减区间；

(2)画出f(x)的图象.

解:(1)f(x)==

=|2x－1|=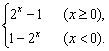

当x≥0时,f(x)=2x－1为单调递增函数；

当x<0时，f(x)=1－2x为单调递减函数.

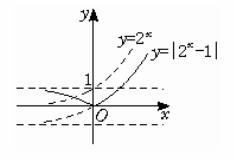
(2)首先作出y=2x的图象，将图象向下平移一个单位，得到y=2x－1的图象，再将y=2x－1的图象在x轴上方的部分不动，x轴下方部分作关于x轴的对称图象，即得函数f(x)=|2x－1|的图象,如图.


练习册系列答案
相关题目
已知函数f(x)=
3x+5，(x≤0)
x+5，(0＜x≤1)
-2x+8，(x＞1)
，
求（1）f(
1
π
)，f[f(-1)]的值；
（2）若f（a）＞2，则a的取值范围．
精英家教网已知函数f(x)=
(1-3a)x+10ax≤7
ax-7x＞7.
是定义域上的递减函数，则实数a的取值范围是（　　）
A、(
1
3
，1)
B、（
1
3
，
1
2
]
C、（
1
3
，
6
11
]
D、[
6
11
，1）
已知函数f(x)=
|x-1|-a
1-x2
是奇函数．则实数a的值为
 
．
已知函数f(x)=
2x-2-x2x+2-x

（1）求f（x）的定义域与值域；
（2）判断f（x）的奇偶性并证明；
（3）研究f（x）的单调性．
已知函数f(x)=
x-1x+a
+ln(x+1)，其中实数a≠1．
（1）若a=2，求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）若f（x）在x=1处取得极值，试讨论f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网